Tentei fazer esse exercício e achei que estava indo bem, mas no fim errei a alternativa. A parti de onde está errado?
Se a diferente de zero, então

eu primeiro fiz o mmc e resolvi a soma do primeiro parênteses e a subtração do segundo:
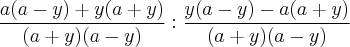
Cortei os "de baixo" porque são iguais e obtive:
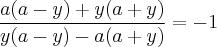
Desenvolvi as distributivas:
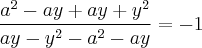

As alternativas são:
a)para todos, exceto dois valores de y
b) só para dois valores de y
c) para todos os valores de y
d) para nenhum valor de y
E como deu tudo igual eu coloquei a alternativa C, mas a certa é a A. Por que? Onde eu errei?
Obrigado!!!


 !
!
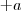 e
e 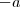 tornar a equação INICIAL impossível, veja,
tornar a equação INICIAL impossível, veja,
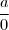 é impossível!!
é impossível!!


 , avisa que eu resolvo.
, avisa que eu resolvo.

