-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478506 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533328 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496828 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 710057 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2129150 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por juniorthai » Qui Fev 11, 2010 08:15
por juniorthai » Qui Fev 11, 2010 08:15
pessoal ..da uma luz ai...
como eu soluciono, passo a passo, a equação..
300+40x-2.300/x-80=300
eu cheguei ai a partir do seguinte problema
a distancia entra curitiba e florianopolis é de 300 km. para cobrir essa distancia a certa velocidade media,um automovel gastou x horas. sabe se que a mesma distancia seria percorrida em duas horas a menos se o veiculo aumentase em 40 km/h a sua velocidade média.qual o tempo x gasto para percorrer os 300 km?
se alguem souber solucionar d outra maneira...tmm serve...rsrsrs.
abraço
-
juniorthai
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Fev 08, 2010 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Fev 11, 2010 10:54
por Molina » Qui Fev 11, 2010 10:54
Bom dia, Junior.
Eu faria usando a definição de velocidade média, que é:

, onde
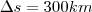
(Distância do percurso).
Então temos que:

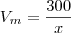 (Já que o tempo percorrido é de x horas)
(Já que o tempo percorrido é de x horas)Dando continuidade ao enunciado temos que:
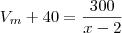 (Já que a velocidade média aumentou em 40 e o tempo diminuiu em 2 horas)
(Já que a velocidade média aumentou em 40 e o tempo diminuiu em 2 horas)Igualando as duas equações ficamos com:

Resolvendo essa equação fracionária chegamos em uma equação do 2° grau e encontramos como raízes 5 e -3. Como o tempo (x) não pode ser negativo, ficamos com

.
Qualquer dúvida informe. Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Qui Fev 11, 2010 12:55
por MarceloFantini » Qui Fev 11, 2010 12:55
Boa tarde.
Pode parecer chato, mas lembre-se que o instante não pode assumir um valor negativo porque a análise do movimento começou em

.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por juniorthai » Qui Fev 11, 2010 14:13
por juniorthai » Qui Fev 11, 2010 14:13
valew...mais eu nao sei como resolve
300/x = (300/ x-2) - 40
-
juniorthai
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Fev 08, 2010 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Fev 11, 2010 14:18
por Molina » Qui Fev 11, 2010 14:18
juniorthai escreveu:valew...mais eu nao sei como resolve
300/x = (300/ x-2) - 40
Tira o mmc de tudo, que será
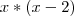
Tenta aí e qualquer coisa avisa!
Bom estudo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por mafissoni » Qui Nov 13, 2014 16:33
por mafissoni » Qui Nov 13, 2014 16:33
preciso de ajuda em velocidade media:
Uma pessoa adulta, caminhando normalmente consegue percorrer 6.250 m em 1h 15 min. qual é a velocidade media preciso da resolução
-
mafissoni
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Nov 13, 2014 16:11
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por lulopes » Sex Dez 08, 2017 20:05
por lulopes » Sex Dez 08, 2017 20:05
COMO EU MONTO UM EXERCICIO DO TIPO ASSIM RAFAELTEM UM IRMÃO 4 ANOS MAIS NOVO E UM IRMÃO 6 ANOS MAIS VELHO.O PRODUTO DOS NUMEROS QUE REPRESENTAM AS IDADES EM ANOS, DOS DOSI IRMÃOS DE RAFAEL É 231. A IDADE DE RAFAEL É UM MULTIPLO DE
-
lulopes
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Dez 08, 2017 19:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagoga
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 6723 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 2926 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 4705 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
-
- equação do 2º grau
por juniorthai » Seg Fev 08, 2010 12:05
- 2 Respostas
- 11047 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:48
Trigonometria
-
- Equação do 1º grau
por gigante2010 » Ter Out 12, 2010 21:19
- 3 Respostas
- 3156 Exibições
- Última mensagem por MarceloFantini

Dom Out 17, 2010 15:25
Tópicos sem Interação (leia as regras)
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , onde
, onde 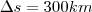 (Distância do percurso).
(Distância do percurso).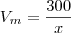
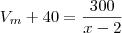

 .
.

 .
.
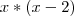
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
