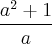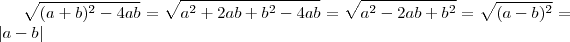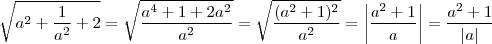por vscarv » Ter Fev 10, 2015 17:25
por vscarv » Ter Fev 10, 2015 17:25
Simplifique:
a)
![\sqrt[2]{(a+b)^{2}-4ab} \sqrt[2]{(a+b)^{2}-4ab}](/latexrender/pictures/8d96c7d183941c8b8b6e48b143824eba.png)
Minha resposta deu a+b-2ab
b)
![\sqrt[2]{a^{2}+\frac{1}{a^{2}}+2} \sqrt[2]{a^{2}+\frac{1}{a^{2}}+2}](/latexrender/pictures/0a0498f358fa9d8660f58a806bc6e532.png)
Minha resposta deu (a^2+1+V2)/a
Respostas:
a) a-b
b)
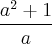
-
vscarv
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Fev 10, 2015 17:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Baltuilhe » Ter Fev 10, 2015 21:11
por Baltuilhe » Ter Fev 10, 2015 21:11
Boa tarde!
a)
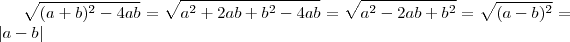
Minha ressalva fica para o fato de ao extrairmos a raiz quadrada de uma expressão, obrigatoriamente a resposta é o módulo desta. Estaria errado dizer que a resposta é a-b, a não ser que tenhamos em algum lugar escrito que a>b.
b)
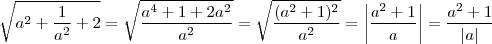
Mesma coisa aqui para o caso da raiz de a ao quadrado. Ao tirar a raiz tive que manter o módulo pois não se se o valor de a é positivo ou não.
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8912 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3257 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8823 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2537 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 4080 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{(a+b)^{2}-4ab} \sqrt[2]{(a+b)^{2}-4ab}](/latexrender/pictures/8d96c7d183941c8b8b6e48b143824eba.png)
![\sqrt[2]{a^{2}+\frac{1}{a^{2}}+2} \sqrt[2]{a^{2}+\frac{1}{a^{2}}+2}](/latexrender/pictures/0a0498f358fa9d8660f58a806bc6e532.png)