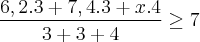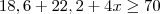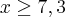por rcpn » Ter Dez 02, 2014 21:11
por rcpn » Ter Dez 02, 2014 21:11
Questão do colégio Pedro II
Vivian estuda no colégio pedro II e, para que seja aprovada sem prova final é necessário que a média das três certificações que compõem o sistema de avaliação seja maior ou igual a sete. A tabela mostra as notas obtidas por Vivian em Matemática e o peso atribuído a cada uma das certificações.
Se
certificações notas peso
primeira 6,2 3
segunda 7,4 3
terceira x 4
a nota mínima que Vivian precisa tirar na terceira certificação para ser aprovada sem prova final é
a) 7,0
b) 7,3
c) 7,4
d) 7,6
sei fazer uma média aritmética ponderada, mas nunca vi um caso onde eu não consigo saber quem seria a 3ª nota. Se alguém puder me ajudar , desde já agradeço
-
rcpn
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Ter Abr 08, 2014 10:46
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: formação geral
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Média Móvel Ponderada
por Danilo Dias Vilela » Qua Mar 16, 2011 22:17
- 1 Respostas
- 6081 Exibições
- Última mensagem por Neperiano

Ter Jul 19, 2011 18:51
Estatística
-
- Média Ponderada Concurso
por kattuloliveira » Ter Jul 04, 2017 01:38
- 0 Respostas
- 4067 Exibições
- Última mensagem por kattuloliveira

Ter Jul 04, 2017 01:38
Aritmética
-
- Média Ponderada, como resolver este caso!
por Rafael2829 » Qua Jan 02, 2013 01:03
- 2 Respostas
- 2595 Exibições
- Última mensagem por Rafael2829

Qua Jan 02, 2013 15:23
Aritmética
-
- Média Aritmética
por gustavowelp » Seg Jun 28, 2010 11:17
- 1 Respostas
- 2375 Exibições
- Última mensagem por Douglasm

Seg Jun 28, 2010 12:09
Estatística
-
- média aritmética
por Cristina Lins » Sex Nov 18, 2011 10:56
- 1 Respostas
- 2075 Exibições
- Última mensagem por DanielFerreira

Seg Nov 28, 2011 20:21
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.