 por Esthevam » Sex Fev 21, 2014 13:20
por Esthevam » Sex Fev 21, 2014 13:20
A fortuna de João foi dividida da seguinte forma. Um quinto para seu irmão mais velho, um sexto do restante para seu irmão mais novo e partes iguais do restante parada cada um de seus 12 filhos. Que fração da fortuna cada filho recebeu?
Gabarito: 1/18. Não consegui fazer nem o início.
-
Esthevam
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 21, 2014 11:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Preparatório Ita
- Andamento: cursando
 por young_jedi » Sex Fev 21, 2014 18:05
por young_jedi » Sex Fev 21, 2014 18:05
a fortuna incial era "x"
o irmão mais velho ficou com x/5 então sobrou
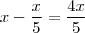
o outro irmao ficou com 1/6 disto ou seja sobrou
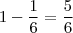
, portanto
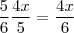
isso foi dividido em 12 partes iguais ou seja
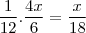
ou seja a decima oitava parte de "x"
1/18
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7470 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3219 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2753 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2717 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2662 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


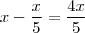
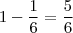 , portanto
, portanto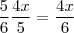
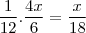


 .
.



