 por b_afa » Qua Nov 20, 2013 16:14
por b_afa » Qua Nov 20, 2013 16:14
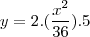
Eu sei toda a álgebra básica mas na hora de isolar uma variável eu me perco e até agora não sei onde estudar isso.
Ele substituiu t nessa equação
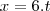
e isolou na segunda
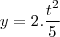
Se alguém puder resolver mostrando a resolução eu agradeço,e se possível me enviem um link com mais exercícios parecidos com este para eu ir treinado (de preferência com resolução).
Obrigado.
-
b_afa
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Nov 15, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando \o/
- Andamento: cursando
 por alienante » Sáb Jan 11, 2014 10:09
por alienante » Sáb Jan 11, 2014 10:09
Olha não é querendo ser arrogante, mas tem certeza que a equação é essa? Porque para isolar o x é deixar ele sozinho,então,

, fica:
![\frac{y}{10}=\frac{x^2}{36}\rightarrow\frac{36y}{10}=x^2\rightarrow x=\sqrt[]{\frac{36y}{10}} \frac{y}{10}=\frac{x^2}{36}\rightarrow\frac{36y}{10}=x^2\rightarrow x=\sqrt[]{\frac{36y}{10}}](/latexrender/pictures/67d83649694d994f0fabffb3319c8827.png)
.
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Livros de Geometria Plana e Álgebra básica.
por andy » Qua Dez 05, 2012 11:14
- 2 Respostas
- 3129 Exibições
- Última mensagem por MarceloFantini

Qua Dez 05, 2012 23:57
Geometria Plana
-
- [Isolar Variável] Ajuda para isolar variável na equação
por Gabriel Gomes » Sex Fev 03, 2012 08:55
- 1 Respostas
- 10707 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 04, 2012 12:51
Sistemas de Equações
-
- ISOLAR B16 NA FORMULA
por VARGASH » Qui Abr 14, 2011 12:40
- 1 Respostas
- 1815 Exibições
- Última mensagem por FilipeCaceres

Qui Abr 14, 2011 15:31
Sistemas de Equações
-
- [Isolar incógnita]
por malukaopba2018 » Ter Mar 27, 2018 06:54
- 2 Respostas
- 4677 Exibições
- Última mensagem por malukaopba2018

Qua Mar 28, 2018 07:08
Equações
-
- Como isolar uma variável?
por Alce » Qui Ago 23, 2012 14:09
- 3 Respostas
- 8764 Exibições
- Última mensagem por MarceloFantini

Qui Ago 23, 2012 17:16
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
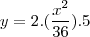
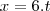 e isolou na segunda
e isolou na segunda 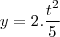


 , fica:
, fica:![\frac{y}{10}=\frac{x^2}{36}\rightarrow\frac{36y}{10}=x^2\rightarrow x=\sqrt[]{\frac{36y}{10}} \frac{y}{10}=\frac{x^2}{36}\rightarrow\frac{36y}{10}=x^2\rightarrow x=\sqrt[]{\frac{36y}{10}}](/latexrender/pictures/67d83649694d994f0fabffb3319c8827.png) .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.