 por chronoss » Seg Abr 22, 2013 21:13
por chronoss » Seg Abr 22, 2013 21:13
Sejam a, b, c, d números reais tais que: a³+b³+c³+d³ = a+b+c+d = 0. Prove que a soma de dois desses números é zero.
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Ter Abr 23, 2013 11:36
por e8group » Ter Abr 23, 2013 11:36
Neste caso podemos proceder da seguinte forma ,

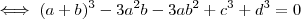
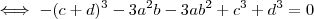
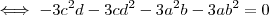
\\
![\iff -3[cd(c +d) + ab(b +a)] = 0 \iff -3[cd(c +d) + ab(b +a)] = 0](/latexrender/pictures/227fc8182aef106ec81ff439e8ed7243.png)
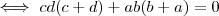
Pela relação
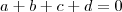
,temos que
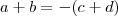
.Assim,
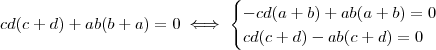
.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8917 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3261 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8824 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2542 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 4084 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



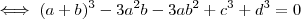
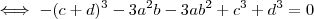
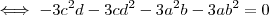 \\
\\ ![\iff -3[cd(c +d) + ab(b +a)] = 0 \iff -3[cd(c +d) + ab(b +a)] = 0](/latexrender/pictures/227fc8182aef106ec81ff439e8ed7243.png)
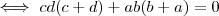
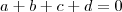 ,temos que
,temos que 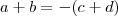 .Assim,
.Assim, 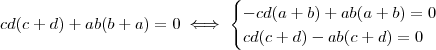 .
. 

 .
.



