-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480045 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538129 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501915 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 723382 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2157564 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por bencz » Dom Mar 03, 2013 12:58
por bencz » Dom Mar 03, 2013 12:58
Olá... estou aqui estudando, e, cai em uma questão, que nao consigo responder, na realidade, nao consigo nem entender como resolver ela.... :(
a questão é:
Considere os conjuntos
K = conjunto dos quadriláteros planos
P = {x ? K | x tem lados 2 a 2 paralelos}
L = {x ? K | x tem 4 lados congruentes}
R = {x ? K | x tem 4 ângulos retos}
Q = {x ? K | x tem 4 lados congruentes e ângulos retos}
Até aí tudo bem, podemos dizer que as citações acima estão todas corretas
Determine os conjuntos:
a) L ? P
b) R ? P
c) L ? R
d) Q ? R
e) L ? Q
f) P U Q
Bom, oq eu entendi é que:
L = Losango
P = Paralelograma
R = retangulo
Q = quadrado
mas, como resolve um treco desse :::Considere os conjuntos
K = conjunto dos quadriláteros planos
P = {x ? K | x tem lados 2 a 2 paralelos}
L = {x ? K | x tem 4 lados congruentes}
R = {x ? K | x tem 4 ângulos retos}
Q = {x ? K | x tem 4 lados congruentes e ângulos retos}
Até aí tudo bem, podemos dizer que as citações acima estão todas corretas
Determine os conjuntos:
a) L ? P
b) R ? P
c) L ? R
d) Q ? R
e) L ? Q
f) P U Q
BOm, oq eu entendi é que:
L = Losango
P = Paralelograma
R = retangulo
Q = quadrado
Mas como que se resolve um treco desse ????? :(
Agradeço a ajuda
-
bencz
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 14, 2011 00:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por maison_souza » Ter Nov 11, 2014 16:02
por maison_souza » Ter Nov 11, 2014 16:02
Ainda entendeu mais do que pois eu não sei nem identificar quem são os elementos dos conjuntos. :(
-
maison_souza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 11, 2014 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Desenvolvimento de Softwar
- Andamento: cursando
 por adauto martins » Ter Nov 11, 2014 20:05
por adauto martins » Ter Nov 11, 2014 20:05
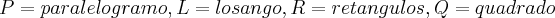
...todos estao contidos em K,todos sao quadrilateros...
a)
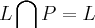
pq,todo losango e um paralelogramo,
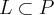
...
b)
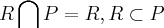
c)
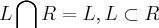
d)
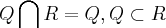
e)
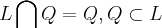
f)
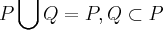
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por maison_souza » Sex Nov 14, 2014 13:15
por maison_souza » Sex Nov 14, 2014 13:15
Bom dia colegas, essa questão se encontra no Livro Fundamentos da Matemática Elementar - Conjuntos, questão 31, não consegui entender por quê que P=paralelogramo,L=losango,R=retângulos,Q=quadrado POIS, isso não está implícito no enunciado. E também se P = paralelogramo ENTÃO
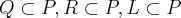
ENTÃO penso que os conjuntos são assim:
K= { paralelogramo, trapézios}
P = {paralelogramo}
L = {quadrado,losango}
R = {retângulo, quadrado}
Q = {quadrado}
-
maison_souza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 11, 2014 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Desenvolvimento de Softwar
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8234 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 5556 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4084 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7336 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [ CONJUNTOS: OPERAÇÕES ENTRE CONJUNTOS ]
por anneliesero » Seg Mar 25, 2013 20:18
- 1 Respostas
- 1684 Exibições
- Última mensagem por DanielFerreira

Sex Mar 29, 2013 02:43
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


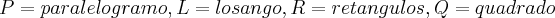 ...todos estao contidos em K,todos sao quadrilateros...
...todos estao contidos em K,todos sao quadrilateros...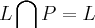 pq,todo losango e um paralelogramo,
pq,todo losango e um paralelogramo, ...
...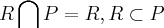
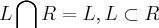
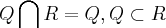
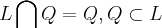
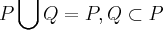

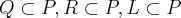 ENTÃO penso que os conjuntos são assim:
ENTÃO penso que os conjuntos são assim:




