Bem, tenho uma equação, da qual eu jah ateh sei o resultadom mas gostaria de saber como foi feito o calculo para chegar no resultado, segue:
equação: 6x^3-4x^2-x-2x^3+2x^2+x
resultado: 4x^3-2x^2
como chegou neste resultado?
obrigado



leonardoandra escreveu:Bem, tenho uma equação, da qual eu jah ateh sei o resultadom mas gostaria de saber como foi feito o calculo para chegar no resultado, segue:
equação: 6x^3-4x^2-x-2x^3+2x^2+x
resultado: 4x^3-2x^2
como chegou neste resultado?
obrigado
 , vamos agrupar e resolver os termos semelhantes:
, vamos agrupar e resolver os termos semelhantes: = { agrupando, juntando os termos semelhantes, neste caso aqueles contendo
= { agrupando, juntando os termos semelhantes, neste caso aqueles contendo  com o mesmo expoente }
com o mesmo expoente }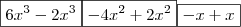 = { resolvendo = somar, subtrair, etc. }
= { resolvendo = somar, subtrair, etc. }


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: