Eu compreendo a definição matemática, formal e correta para a soma e para a subtração. P. ex., 3 + 3 é a mesma coisa de unir um 2 conjuntos com 3 elementos cada e conjuto resultante terá 6 elementos.
Agora, na multiplicação, dizem que 3 vezes 5 é mesma coisa que 5 mais 5 mais 5, 3 vezes. Mas isso é apenas uma coincidência, pq os fatores são Natutais, e se fossem raízes, por ex: ²?2 vezes ³?3, eae?
Nem vou entrar em detalhes nas outras operações pq meu questionamento é análogo ao da multiplicação.
Gostaria de maiores esclarecimento, obg.


 é um conjunto com três elementos, então
é um conjunto com três elementos, então 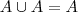 . Veja os
. Veja os 


 .
.
 :
: