 por jose henrique » Ter Out 26, 2010 23:30
por jose henrique » Ter Out 26, 2010 23:30
Estou em dúvida na resolução deste exercício, pois no denominador apareceu um módulo, resolvi desta maneira e gostaria de saber se fiz algo errado.
Considerei que x tenha um valor absoluto e positivo.
![\frac{\sqrt[]{32{x}^{4}+16{x}^{2}}}{4\left|x \right|} = \frac{\sqrt[]{16{x}^{2}\left(2{x}^{2}+1 \right)}}{4x}=\frac{4x\sqrt[]{2{x}^{2}+1}}{4x}=\sqrt[]{2{x}^{2}+1}=2X\sqrt[]{1} \frac{\sqrt[]{32{x}^{4}+16{x}^{2}}}{4\left|x \right|} = \frac{\sqrt[]{16{x}^{2}\left(2{x}^{2}+1 \right)}}{4x}=\frac{4x\sqrt[]{2{x}^{2}+1}}{4x}=\sqrt[]{2{x}^{2}+1}=2X\sqrt[]{1}](/latexrender/pictures/566c75710fdff2f449209139a5d279d3.png)
Obrigado desde já pela atenção!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por MarceloFantini » Qua Out 27, 2010 04:36
por MarceloFantini » Qua Out 27, 2010 04:36
Você não pode tirar o módulo, lembre-se que
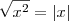
. Então
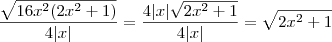
e pára por aí.

NÃO É IGUAL A
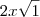
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jose henrique » Qua Out 27, 2010 07:28
por jose henrique » Qua Out 27, 2010 07:28
obrigado!!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8929 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3263 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8831 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2549 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 4095 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[]{32{x}^{4}+16{x}^{2}}}{4\left|x \right|} = \frac{\sqrt[]{16{x}^{2}\left(2{x}^{2}+1 \right)}}{4x}=\frac{4x\sqrt[]{2{x}^{2}+1}}{4x}=\sqrt[]{2{x}^{2}+1}=2X\sqrt[]{1} \frac{\sqrt[]{32{x}^{4}+16{x}^{2}}}{4\left|x \right|} = \frac{\sqrt[]{16{x}^{2}\left(2{x}^{2}+1 \right)}}{4x}=\frac{4x\sqrt[]{2{x}^{2}+1}}{4x}=\sqrt[]{2{x}^{2}+1}=2X\sqrt[]{1}](/latexrender/pictures/566c75710fdff2f449209139a5d279d3.png)

![\frac{\sqrt[]{32{x}^{4}+16{x}^{2}}}{4\left|x \right|} = \frac{\sqrt[]{16{x}^{2}\left(2{x}^{2}+1 \right)}}{4x}=\frac{4x\sqrt[]{2{x}^{2}+1}}{4x}=\sqrt[]{2{x}^{2}+1}=2X\sqrt[]{1} \frac{\sqrt[]{32{x}^{4}+16{x}^{2}}}{4\left|x \right|} = \frac{\sqrt[]{16{x}^{2}\left(2{x}^{2}+1 \right)}}{4x}=\frac{4x\sqrt[]{2{x}^{2}+1}}{4x}=\sqrt[]{2{x}^{2}+1}=2X\sqrt[]{1}](/latexrender/pictures/566c75710fdff2f449209139a5d279d3.png)

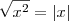 . Então
. Então 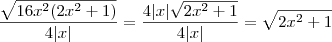 e pára por aí.
e pára por aí.  NÃO É IGUAL A
NÃO É IGUAL A 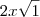 .
.

