Olá
marcella_mat08, boa tarde, seja bem-vinda!
Para eliminar eventuais confusões com o símbolo de inclusão

, favor conferir o enunciado.
O que você "escreveu" fica desta forma:
a)

b)

c)

d)

e)

f)

Sobre a notação:

A é subconjunto de B
ou
A está contido em B
ou
A é parte de B

B contém A
Quando queremos provar que dois conjuntos são iguais, por exemplo,

, precisamos mostrar que todo elemento de

pertence a

e, reciprocamente, todo elemento de

pertence a

. A notação fica assim:

Esta definição diz que todo elemento de

é elemento de

e vice-versa, isto é,

e
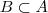
, portanto, também podemos considerar a condição de igualdade assim:

Assim, para provarmos que

devemos provar que

e
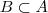
.
Veja também em seu material as definições da diferença e de complementar entre conjuntos!
Bons estudos!


 , favor conferir o enunciado.
, favor conferir o enunciado.







 , precisamos mostrar que todo elemento de
, precisamos mostrar que todo elemento de  pertence a
pertence a  e, reciprocamente, todo elemento de
e, reciprocamente, todo elemento de 
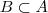 , portanto, também podemos considerar a condição de igualdade assim:
, portanto, também podemos considerar a condição de igualdade assim:
