Seja p(x)=x^2+px+p uma função real na variável real.Os valores de p para os quais f(x)=0 possue raiz dupla positiva são:
a) 0<p<4
b) p=4
c) p=0
d) f(x)=0 não pode ter raiz dupla positiva
e) n.r.a



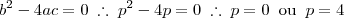

 um polinômio tal que
um polinômio tal que 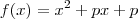 . Seja
. Seja  a raiz dupla de
a raiz dupla de  , então a primeira derivada de
, então a primeira derivada de  no ponto
no ponto  é nula, isto é:
é nula, isto é: 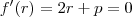 , assim
, assim 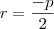 é a raiz dupla.
é a raiz dupla. é raiz, então:
é raiz, então: 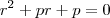 , isto é,
, isto é, 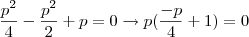 e como
e como 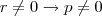 e decore em
e decore em  .
. um polinômio ta que
um polinômio ta que 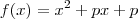 . Seja
. Seja  a raiz dupla de
a raiz dupla de  , pelas relações de Girard, temos:
, pelas relações de Girard, temos: e
e 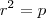 e dessas obtemos:
e dessas obtemos: 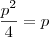 e como
e como 
 adimite raiz dupla e é um polinômio do segundo grau, então
adimite raiz dupla e é um polinômio do segundo grau, então  pode ser reduzido a um quadrado perfeito de forma canônica:
pode ser reduzido a um quadrado perfeito de forma canônica: 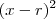 , tal que
, tal que  é sua raiz. Assim,
é sua raiz. Assim, 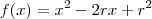 . Fazendo a identidade polinomial entre o polinômio supracitado e o fornecido pelo enunciado, obtemos:
. Fazendo a identidade polinomial entre o polinômio supracitado e o fornecido pelo enunciado, obtemos: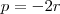 e
e  e dessas relalçõs surge:
e dessas relalçõs surge: 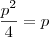 e como
e como 

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)