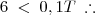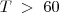por Karina » Sáb Mai 29, 2010 17:31
por Karina » Sáb Mai 29, 2010 17:31
A relação
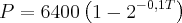
descreve o crescimento de uma população de microorganismos T dias após o instante
zero. O valor de P é superior a 6300 se, e somente se, T satisfazer a condição
a) 2<t<16
b) t<60
c) t<30
d) t>60
e) 32<t<64
Eu consegui resolver por substituição dos valores das respostas na inequação
mas isso demora muito, alguem consegue resolver essa inequação?
-
Karina
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Fev 09, 2010 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Enfermagem
- Andamento: cursando
 por Karina » Seg Mai 31, 2010 15:08
por Karina » Seg Mai 31, 2010 15:08
A resposta correta é a D. T>60
-
Karina
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Fev 09, 2010 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Enfermagem
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequação exponencial
por Aliocha Karamazov » Seg Abr 11, 2011 22:46
- 2 Respostas
- 1641 Exibições
- Última mensagem por Aliocha Karamazov

Seg Abr 11, 2011 23:11
Funções
-
- [inequação exponencial]
por paola-carneiro » Sáb Abr 07, 2012 18:03
- 2 Respostas
- 4897 Exibições
- Última mensagem por paola-carneiro

Sáb Abr 07, 2012 18:54
Funções
-
- Inequação Exponencial
por Rafael16 » Qui Jul 26, 2012 21:22
- 1 Respostas
- 1157 Exibições
- Última mensagem por DanielFerreira

Qui Jul 26, 2012 21:32
Funções
-
- inequação exponencial
por Danilo » Sáb Ago 25, 2012 01:34
- 2 Respostas
- 1563 Exibições
- Última mensagem por Danilo

Sáb Ago 25, 2012 01:50
Álgebra Elementar
-
- Inequação Exponencial
por Rafael16 » Seg Jun 17, 2013 22:54
- 2 Respostas
- 1801 Exibições
- Última mensagem por Rafael16

Ter Jun 18, 2013 10:40
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
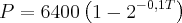 descreve o crescimento de uma população de microorganismos T dias após o instante
descreve o crescimento de uma população de microorganismos T dias após o instante

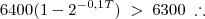
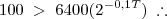
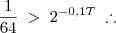
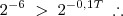
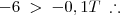
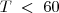

![[-6 \; > \; -0,1T] . (-1) \; \therefore [-6 \; > \; -0,1T] . (-1) \; \therefore](/latexrender/pictures/de896caaf8b3995cd28267e2ccc663e4.png)