-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478917 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536833 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 500559 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 720315 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2147408 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por adauto martins » Seg Mai 28, 2018 18:49
por adauto martins » Seg Mai 28, 2018 18:49
seja a equaçao diofantina:
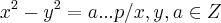
,mostre que a é impar.
soluçao:
para q. a equaçao tenha soluçao teremos q. ter:
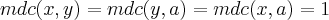
,ou seja:
primos dois a dois...logo,nao poderemos ter ambos
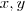
pares.
e nem ambos impares,pois:se forem pares mdc(x,y) sera multiplo de 2 e refuta a condiçao de soluçao.se forem impares teriamos:
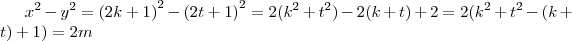
,q ´um numero par,e portanto divisivel por 2,o q. refuta a condiçao(mdc(x,y)=1) de termos soluçoes inteiras p. a equaçao diofantina dada.portanto a ,somente podera ser impar.
ou entao,
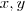
tem q. ser um par,outro impar.entao:
suporemos x,impar e y,par,logo:

raciocinio analogo p/

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Jun 04, 2018 19:54
por adauto martins » Seg Jun 04, 2018 19:54
para ficar mais clara a condiçao de q. o par(x,y) nao poderem ser ambos impares,
usarei a ALGEBRA MODULAR.
todo impar quadradro é escrito como
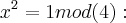
,x impar.
prova:
seja x um impar,logo:
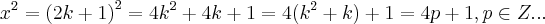
,ou seja:
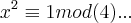
,entao:
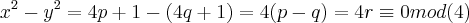
q. contradiz a condiçao exposta acima...
obs:

é tbem um impar quadrado,ou seja:
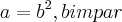
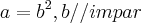
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fundamento da Matemática] Equaçõesw Diofantinas
por andrecalegarif » Ter Jul 25, 2017 00:54
- 1 Respostas
- 1775 Exibições
- Última mensagem por adauto martins

Sáb Jul 29, 2017 16:37
Aritmética
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6097 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 10844 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 14785 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 3941 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 45 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
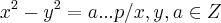 ,mostre que a é impar.
,mostre que a é impar.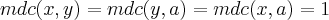 ,ou seja:
,ou seja: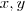 pares.
pares.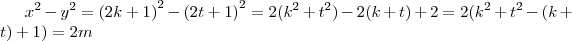 ,q ´um numero par,e portanto divisivel por 2,o q. refuta a condiçao(mdc(x,y)=1) de termos soluçoes inteiras p. a equaçao diofantina dada.portanto a ,somente podera ser impar.
,q ´um numero par,e portanto divisivel por 2,o q. refuta a condiçao(mdc(x,y)=1) de termos soluçoes inteiras p. a equaçao diofantina dada.portanto a ,somente podera ser impar.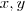 tem q. ser um par,outro impar.entao:
tem q. ser um par,outro impar.entao:



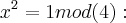 ,x impar.
,x impar. 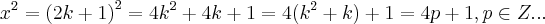 ,ou seja:
,ou seja: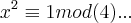 ,entao:
,entao: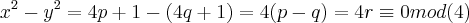 q. contradiz a condiçao exposta acima...
q. contradiz a condiçao exposta acima... é tbem um impar quadrado,ou seja:
é tbem um impar quadrado,ou seja: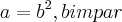
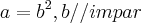 ...
...