Gostaria de tirar algumas dúvidas sobre propriedades de potenciação.
Vamos lá:
Como somar/subtrair potências de bases iguais e expoentes diferentes?
Ou seja, como resolver algo do tipo:
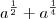 SEM TRANSFORMAR EM RAIZ, SE FOR O CASO.
SEM TRANSFORMAR EM RAIZ, SE FOR O CASO.Ex:
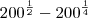
Como somar/subtrair potências de bases diferentes e expoentes iguais?
Ou seja, como resolver algo do tipo:
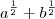 SEM TRANSFORMAR EM RAIZ, SE FOR O CASO.
SEM TRANSFORMAR EM RAIZ, SE FOR O CASO.Ex:
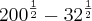
Como somar/subtrair potências de bases diferentes e expoentes diferentes?
Ou seja, como resolver algo do tipo: a^\frac{1}{2} ± b^\frac{1}{4} SEM TRANSFORMAR EM RAIZ, SE FOR O CASO.
Ex:
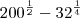
Att.


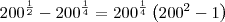
![{200}^{\frac{1}{4}}\left({200}^{2} - 1 \right) = 39999 \times {200}^{\frac{1}{4}} \;\;\;\;[1] {200}^{\frac{1}{4}}\left({200}^{2} - 1 \right) = 39999 \times {200}^{\frac{1}{4}} \;\;\;\;[1]](/latexrender/pictures/8b87b7bccb78be94787893d4e9ca99e5.png)
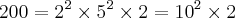
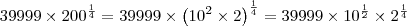
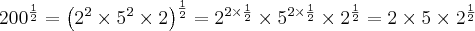
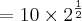
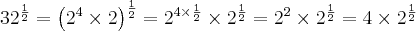
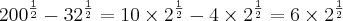

![{200}^{\frac{1}{4}}\left({200}^{2} - 1 \right) = 39999 \times {200}^{\frac{1}{2}} \;\;\;\;[1] {200}^{\frac{1}{4}}\left({200}^{2} - 1 \right) = 39999 \times {200}^{\frac{1}{2}} \;\;\;\;[1]](/latexrender/pictures/21b2fd2d6475aa34a2029e549d487bd3.png) "
"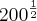 , não seria
, não seria 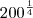 ?
?![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.