 por Luanna » Qui Fev 11, 2010 09:46
por Luanna » Qui Fev 11, 2010 09:46
Olá , gostaria que alguem me ajudasse a fatorar estas expressões , porque eu esqueci completamente como se fatora ! Obrigada !

a ) 4ax - 8ay
b ) x² - 64
c ) x² + 6x - 9
d ) 81 a² - 18a +1
-
Luanna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Nov 10, 2009 15:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 10:27
por Molina » Qui Fev 11, 2010 10:27
Bom dia.
a)
 Você vai colocar em evidência o que há em comum nos dois termos e dentro do parênteses o que há de diferente entre eles. É o passo contrário da distributiva. Note que 8=2*4, então ficaria assim:
Você vai colocar em evidência o que há em comum nos dois termos e dentro do parênteses o que há de diferente entre eles. É o passo contrário da distributiva. Note que 8=2*4, então ficaria assim: 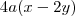 [Fazendo a distributiva (chuveirinho) você volta na expressão original]
[Fazendo a distributiva (chuveirinho) você volta na expressão original]b)
 Diferença de dois quadrados. Note que ambos os termos estão sendo elevados ao quadrado. Neste caso 64=8². Então você vai tirar a raiz do primeiro e do segundo, colocando-os dentro do parênteses com os sinais do meio trocado, assim:
Diferença de dois quadrados. Note que ambos os termos estão sendo elevados ao quadrado. Neste caso 64=8². Então você vai tirar a raiz do primeiro e do segundo, colocando-os dentro do parênteses com os sinais do meio trocado, assim:
c)
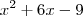 Trinômio quadrado perfeito. Você irá tirar a raiz do primeiro termo e do terceiro termo, e pegar o sinal do segundo termo. Colocar isso dentro de um parênteses e elevar ao quadrado, assim:
Trinômio quadrado perfeito. Você irá tirar a raiz do primeiro termo e do terceiro termo, e pegar o sinal do segundo termo. Colocar isso dentro de um parênteses e elevar ao quadrado, assim: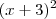 [Note que
[Note que ![(x+3)^2=(x+3)*(x+3)=x^2+6x-9] (x+3)^2=(x+3)*(x+3)=x^2+6x-9]](/latexrender/pictures/d8828a1b1f77d826843cee056fcf2bf2.png)
A letra d) é a mesma sistemática da c), o que muda é o sinal, que vai ser negativo. Consegue fazer?
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Luanna » Qui Fev 11, 2010 10:38
por Luanna » Qui Fev 11, 2010 10:38
Consigo ! Muito Obrigada !

-
Luanna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Nov 10, 2009 15:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Qui Fev 11, 2010 12:53
por MarceloFantini » Qui Fev 11, 2010 12:53
Boa tarde.
Acredito que na letra

ficaria assim:

Pois um trinômio quadrado perfeito é da forma
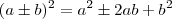
.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Luanna » Qui Fev 11, 2010 23:57
por Luanna » Qui Fev 11, 2010 23:57
ahhh obrigada !
-
Luanna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Nov 10, 2009 15:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LIMITE COM RADICAIS como fatorar ou simplificar
por pedroklein+1978 » Ter Abr 25, 2017 18:42
- 0 Respostas
- 2868 Exibições
- Última mensagem por pedroklein+1978

Ter Abr 25, 2017 18:42
Cálculo: Limites, Derivadas e Integrais
-
- Expressão
por geriane » Qui Abr 22, 2010 12:49
- 4 Respostas
- 3894 Exibições
- Última mensagem por geriane

Sáb Abr 24, 2010 10:50
Trigonometria
-
- Expressão em PG
por Carolziiinhaaah » Qua Jun 16, 2010 21:10
- 1 Respostas
- 2009 Exibições
- Última mensagem por MarceloFantini

Qua Jun 16, 2010 21:39
Progressões
-
- EXPRESSAO
 por JOHNY » Dom Set 05, 2010 15:26
por JOHNY » Dom Set 05, 2010 15:26
- 1 Respostas
- 2094 Exibições
- Última mensagem por MarceloFantini

Seg Set 06, 2010 13:14
Álgebra Elementar
-
- expressão
por jose henrique » Qua Fev 16, 2011 18:16
- 11 Respostas
- 7750 Exibições
- Última mensagem por jose henrique

Seg Fev 28, 2011 19:39
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



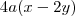 [Fazendo a distributiva (chuveirinho) você volta na expressão original]
[Fazendo a distributiva (chuveirinho) você volta na expressão original]

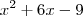
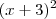 [Note que
[Note que ![(x+3)^2=(x+3)*(x+3)=x^2+6x-9] (x+3)^2=(x+3)*(x+3)=x^2+6x-9]](/latexrender/pictures/d8828a1b1f77d826843cee056fcf2bf2.png)




 ficaria assim:
ficaria assim:
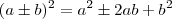 .
.

