Olá! Alguém pode me ajudar, por favor?
Como simplifico essa fração algébrica?
Sei que no numerador tenho uma diferença entre quadrados e no denominador um diferença entre cubos. Fiz assim:
Numerador:
m³ - 1 = (m - 1)(m² + m + 1)
Denominador
m^6 - 1 = (m²)³ - (1)³ = (m² - 1)(m^4 + m² + 1) = [(m + 1)(m - 1)]( m^4 + m² + 1 )
Simplifiquei (m - 1) do numerador com o (m - 1) do denominador, ficando assim:
(m² + m + 1)/ (m + 1)( m^4 + m² + 1 )
Não consigo sair disso :/
O que fiz de errado?


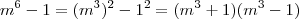
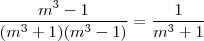
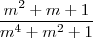 obterá
obterá 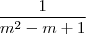 e, portanto, o resultado será
e, portanto, o resultado será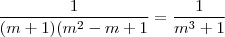 .
.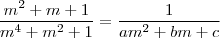
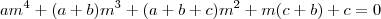

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)