 por Bruna_Ferreira » Seg Jan 05, 2015 16:18
por Bruna_Ferreira » Seg Jan 05, 2015 16:18
Como eu consigo resolver esse exercício???
Existe um grupo G, de ordem 4, com geradores x e y tais que x^2=y^2=e xy=yx. Determine todos os subgrupos de G. Mostre que G={e, x, y, xy}.
-
Bruna_Ferreira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jan 05, 2015 16:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Matemática
- Andamento: cursando
 por adauto martins » Sex Jan 09, 2015 16:05
por adauto martins » Sex Jan 09, 2015 16:05
G e um grupo abeliano isomorfo a
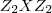
,e nao isomorfo a
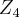
(prove como exercicio),pois
![x.y=y.x...\left[x \right]=\left[y \right]= x.y=y.x...\left[x \right]=\left[y \right]=](/latexrender/pictures/99eb78b12b08c4810379193c04ddc518.png)
{
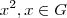
}={
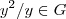
}...logo <G>={
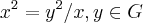
}
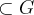
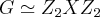
(prove como exercicio)...
sejam
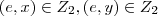
,o q. e possivel pois
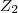
e
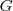
sao abelianos,G por hipotese...entao
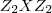
={
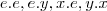
}={
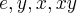
}={e,x,y,xy}
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teoria de grupos
por Luiz Augusto Prado » Seg Mai 30, 2011 21:37
- 1 Respostas
- 1398 Exibições
- Última mensagem por Luiz Augusto Prado

Ter Mai 31, 2011 19:21
Álgebra Elementar
-
- [Teoria dos Grupos] Derivar Teorema
por Imscatman » Qua Fev 19, 2014 18:46
- 1 Respostas
- 1169 Exibições
- Última mensagem por Imscatman

Qui Fev 20, 2014 00:11
Lógica
-
- Demonstrações
por anamendes » Sáb Abr 28, 2012 13:02
- 1 Respostas
- 1215 Exibições
- Última mensagem por LuizAquino

Sáb Abr 28, 2012 14:29
Trigonometria
-
- [complexos] demonstrações
por alentejana » Ter Mai 22, 2012 16:22
- 7 Respostas
- 3509 Exibições
- Última mensagem por joaofonseca

Ter Mai 22, 2012 20:25
Números Complexos
-
- Demonstrações Duvidas
por Razoli » Qui Ago 08, 2013 22:35
- 1 Respostas
- 1129 Exibições
- Última mensagem por e8group

Sex Ago 09, 2013 10:23
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



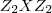 ,e nao isomorfo a
,e nao isomorfo a 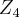 (prove como exercicio),pois
(prove como exercicio),pois ![x.y=y.x...\left[x \right]=\left[y \right]= x.y=y.x...\left[x \right]=\left[y \right]=](/latexrender/pictures/99eb78b12b08c4810379193c04ddc518.png) {
{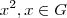 }={
}={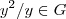 }...logo <G>={
}...logo <G>={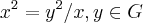 }
}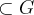
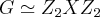 (prove como exercicio)...
(prove como exercicio)...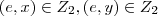 ,o q. e possivel pois
,o q. e possivel pois 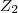 e
e 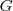 sao abelianos,G por hipotese...entao
sao abelianos,G por hipotese...entao 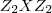 ={
={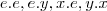 }={
}={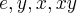 }={e,x,y,xy}
}={e,x,y,xy}