 por IlgssonBraga » Sáb Jul 26, 2014 15:30
por IlgssonBraga » Sáb Jul 26, 2014 15:30
Sejam
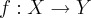
e
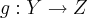
funções. Demonstre que:
Se gof é injetora e f é sobrejetora, então g é injetora. Onde gof=g(f(x)).
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por ant_dii » Sáb Jul 26, 2014 16:32
por ant_dii » Sáb Jul 26, 2014 16:32
Por definição, como

é sobrejetora, para qualquer
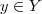
existe, pelo menos, um
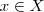
tal que
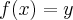
.
Também por definição, como
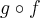
é injetora segue que para
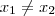
em

implica que
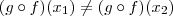
em
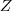
.
Mas
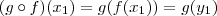
e

para
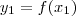
e
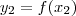
.
Logo,
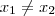
em

implica que
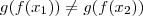
em
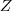
, ou seja,

é injetora. Note que

"cobre" todos os elementos de

, por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de

.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por IlgssonBraga » Sáb Jul 26, 2014 16:42
por IlgssonBraga » Sáb Jul 26, 2014 16:42
Muito obrigado !!!
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função - Como proceder nesse caso?
por micheel » Dom Ago 18, 2013 22:37
- 1 Respostas
- 1994 Exibições
- Última mensagem por Russman

Dom Ago 18, 2013 23:16
Funções
-
- Como proceder... estou com duvidas...
por Netolucena » Dom Mar 18, 2012 18:32
- 2 Respostas
- 1667 Exibições
- Última mensagem por Netolucena

Dom Mar 18, 2012 22:06
Cálculo: Limites, Derivadas e Integrais
-
- analise real como proceder
por caciano-death » Sex Ago 25, 2017 17:56
- 2 Respostas
- 2131 Exibições
- Última mensagem por adauto martins

Qua Ago 30, 2017 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo problemas desse tipo?
por PriscilaMG » Dom Nov 22, 2009 12:25
- 1 Respostas
- 1906 Exibições
- Última mensagem por PriscilaMG

Dom Nov 22, 2009 12:33
Logaritmos
-
- como resolver esse tipo de conta?
por LuizCarlos » Seg Jul 11, 2011 00:43
- 11 Respostas
- 6180 Exibições
- Última mensagem por LuizCarlos

Ter Jul 12, 2011 20:00
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
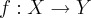 e
e 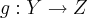 funções. Demonstre que:
funções. Demonstre que:
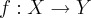 e
e 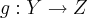 funções. Demonstre que:
funções. Demonstre que:
 é sobrejetora, para qualquer
é sobrejetora, para qualquer 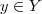 existe, pelo menos, um
existe, pelo menos, um 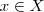 tal que
tal que 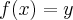 .
.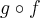 é injetora segue que para
é injetora segue que para 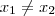 em
em  implica que
implica que 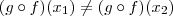 em
em 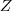 .
.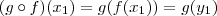 e
e  para
para 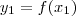 e
e 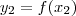 .
.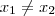 em
em  implica que
implica que 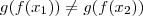 em
em 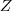 , ou seja,
, ou seja,  é injetora. Note que
é injetora. Note que  "cobre" todos os elementos de
"cobre" todos os elementos de  , por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de
, por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de  .
.

