 por IsadoraLG » Qua Mai 21, 2014 01:17
por IsadoraLG » Qua Mai 21, 2014 01:17
-
IsadoraLG
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Ter Ago 27, 2013 18:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão em Recursos Humanos
- Andamento: formado
 por Russman » Qua Mai 21, 2014 19:55
por Russman » Qua Mai 21, 2014 19:55
É só usar a seguinte propriedade para Reais quaisquer

,

e

:
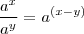
De fato,
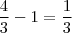
e, portanto,
![\frac{a^{\frac{4}{3}}}{a} = a^{\frac{1}{3}} = \sqrt[3]{a} \frac{a^{\frac{4}{3}}}{a} = a^{\frac{1}{3}} = \sqrt[3]{a}](/latexrender/pictures/c1690934ab3ebe81f63d6b23bd66b604.png)
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por IsadoraLG » Qua Mai 21, 2014 21:36
por IsadoraLG » Qua Mai 21, 2014 21:36
Puxa vida, era uma propriedade simples! =p
Valeu!
Consegui!
E usei o esquema dos números primos para fazer a conta com os expoentes em fração, que você explicou, ao invés do chatinho mmc, bem melhor.
-
IsadoraLG
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Ter Ago 27, 2013 18:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão em Recursos Humanos
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- qual é a integral indefinida passo-a-passo de:
por Raphison » Seg Dez 01, 2014 10:53
- 2 Respostas
- 1630 Exibições
- Última mensagem por Raphison

Qua Dez 03, 2014 08:42
Cálculo: Limites, Derivadas e Integrais
-
- [Desafio] Qual o próximo número?
por victorff7 » Sex Out 28, 2011 13:01
- 1 Respostas
- 3600 Exibições
- Última mensagem por Neperiano

Sex Out 28, 2011 15:07
Desafios Fáceis
-
- Potenciação e Radiciação
por Carlos22 » Qua Abr 13, 2011 22:06
- 1 Respostas
- 1930 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:27
Logaritmos
-
- [Potenciação e radiciação]
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:19
- 4 Respostas
- 2669 Exibições
- Última mensagem por SCHOOLGIRL+T

Sex Nov 09, 2012 23:44
Álgebra Elementar
-
- [Potenciação e Radiciação]
por JU201015 » Seg Nov 12, 2012 22:06
- 2 Respostas
- 1952 Exibições
- Última mensagem por JU201015

Ter Nov 13, 2012 09:08
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{\frac{a}{\sqrt[3]{a}}} \sqrt[]{\frac{a}{\sqrt[3]{a}}}](/latexrender/pictures/a4e36dc82b6f3f10930fde7495098a6a.png) encontramos:
encontramos:![\sqrt[3]{a} \sqrt[3]{a}](/latexrender/pictures/76b1e479f805bb036a3487aeb35932e5.png)
![\frac{\sqrt[]{a}}{\sqrt[]{\sqrt[3]{a}}} \frac{\sqrt[]{a}}{\sqrt[]{\sqrt[3]{a}}}](/latexrender/pictures/977457acefef1f38d93e8b53afb3374b.png) =
=![\frac{\sqrt[]{a}}{\sqrt[6]{a}} \frac{\sqrt[]{a}}{\sqrt[6]{a}}](/latexrender/pictures/8dcf7dc22c33d919cf10468796d92880.png) =
= ![\frac{\sqrt[]{a}}{\sqrt[6]{a}} . \frac{\sqrt[6]{{a}^{5}}}{\sqrt[6]{{a}^{5}}} \frac{\sqrt[]{a}}{\sqrt[6]{a}} . \frac{\sqrt[6]{{a}^{5}}}{\sqrt[6]{{a}^{5}}}](/latexrender/pictures/48a2c78476571390da7e93dba194ad19.png)
![= \frac{\sqrt[]{a}.\sqrt[6]{{a}^{5}}}{a} = \frac{\sqrt[]{a}.\sqrt[6]{{a}^{5}}}{a}](/latexrender/pictures/ec0ea0deccd7ea548447ff81a309ea0b.png)
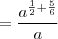
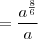
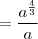

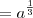
![= \sqrt[3]{a} = \sqrt[3]{a}](/latexrender/pictures/73550eecfea393b1bbcf2475335649ea.png)

![\sqrt[]{\frac{a}{\sqrt[3]{a}}} \sqrt[]{\frac{a}{\sqrt[3]{a}}}](/latexrender/pictures/a4e36dc82b6f3f10930fde7495098a6a.png) encontramos:
encontramos:![\sqrt[3]{a} \sqrt[3]{a}](/latexrender/pictures/76b1e479f805bb036a3487aeb35932e5.png)
![\frac{\sqrt[]{a}}{\sqrt[]{\sqrt[3]{a}}} \frac{\sqrt[]{a}}{\sqrt[]{\sqrt[3]{a}}}](/latexrender/pictures/977457acefef1f38d93e8b53afb3374b.png) =
=![\frac{\sqrt[]{a}}{\sqrt[6]{a}} \frac{\sqrt[]{a}}{\sqrt[6]{a}}](/latexrender/pictures/8dcf7dc22c33d919cf10468796d92880.png) =
= ![\frac{\sqrt[]{a}}{\sqrt[6]{a}} . \frac{\sqrt[6]{{a}^{5}}}{\sqrt[6]{{a}^{5}}} \frac{\sqrt[]{a}}{\sqrt[6]{a}} . \frac{\sqrt[6]{{a}^{5}}}{\sqrt[6]{{a}^{5}}}](/latexrender/pictures/48a2c78476571390da7e93dba194ad19.png)
![= \frac{\sqrt[]{a}.\sqrt[6]{{a}^{5}}}{a} = \frac{\sqrt[]{a}.\sqrt[6]{{a}^{5}}}{a}](/latexrender/pictures/ec0ea0deccd7ea548447ff81a309ea0b.png)
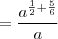
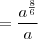
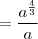

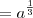
![= \sqrt[3]{a} = \sqrt[3]{a}](/latexrender/pictures/73550eecfea393b1bbcf2475335649ea.png)

 ,
,  e
e  :
: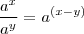
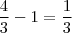
![\frac{a^{\frac{4}{3}}}{a} = a^{\frac{1}{3}} = \sqrt[3]{a} \frac{a^{\frac{4}{3}}}{a} = a^{\frac{1}{3}} = \sqrt[3]{a}](/latexrender/pictures/c1690934ab3ebe81f63d6b23bd66b604.png)







