Seja a e b números inteiros.
Prove que a² = 0, então a = 0.
Dúvida:
se considero a² = a * a e sendo a * a = 0, se dividir ambos por a, vou ter uma indeterminação? pois a = 0.



![{a}^{2} = 0 \rightarrow \sqrt[2]{{a}^{2}} = \sqrt[2]{0} \rightarrow \left|a \right| = 0 \rightarrow a = 0 {a}^{2} = 0 \rightarrow \sqrt[2]{{a}^{2}} = \sqrt[2]{0} \rightarrow \left|a \right| = 0 \rightarrow a = 0](/latexrender/pictures/fe8e3663a1c07292c9bbabf417956651.png) .
.

Pessoa Estranha escreveu:Olá !
Sim, você obterá uma indeterminação. Dentre várias maneiras de resolver, eu faria assim:.
Espero ter ajudado.

 , e assim existe
, e assim existe 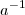 tal que
tal que 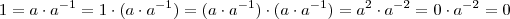 ,contradição .
,contradição . 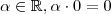 pois ,
pois , 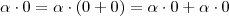 .
.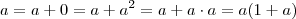 . Daí segue pela unicidade do elemento neutro da multiplicação que
. Daí segue pela unicidade do elemento neutro da multiplicação que 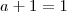 que novamente por unicidade ,desta vez do
que novamente por unicidade ,desta vez do  que resulta
que resulta  .
.
santhiago escreveu:Há varias formas . Uma delas supor absurdo que, e assim existe
tal que
,contradição .
Nota para quaisquerpois ,
.
Alternativamente ,pelo elemento neutro aditivo. Daí segue pela unicidade do elemento neutro da multiplicação que
que novamente por unicidade ,desta vez do
que resulta
.

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)