 por thadeu » Qui Nov 19, 2009 11:41
por thadeu » Qui Nov 19, 2009 11:41
Quantos são os números inteiros p tais que
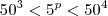
?
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Molina » Qui Nov 19, 2009 13:14
por Molina » Qui Nov 19, 2009 13:14
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por thadeu » Qui Nov 19, 2009 13:46
por thadeu » Qui Nov 19, 2009 13:46
Beleza Molina!
Eu só não consegui entender as duas últimas linhas.
Esses exercícios são de uma lista que me passaram e eu achei interessante colocar no site para que possamos ver diferentes maneiras de resolução.
Eu resolvi essa questão da seguinte maneira:
Fazendo
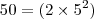
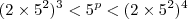
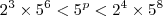
Dividindo todos por

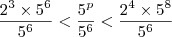
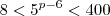
Entre 8 e 400 as seguintes potências de base 5:
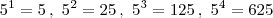
Repare que apenas
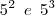
estão entre 8 e 400.


Resposta igual a 2.
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6396 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
- 3 Respostas
- 2690 Exibições
- Última mensagem por PedroSantos

Qua Jan 05, 2011 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Numeros inteiros
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
- 15 Respostas
- 9707 Exibições
- Última mensagem por Raphael Feitas10

Qua Jan 19, 2011 00:40
Números Complexos
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2896 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
-
- Numeros inteiros 3
por Raphael Feitas10 » Qua Jan 19, 2011 17:03
- 1 Respostas
- 1662 Exibições
- Última mensagem por Molina

Qua Jan 19, 2011 21:49
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
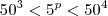 ?
?

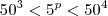 ?
?
?
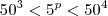
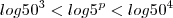
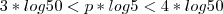
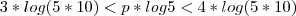
![3*[log5 + log10]<p*log5<4*[log5 + log10] 3*[log5 + log10]<p*log5<4*[log5 + log10]](/latexrender/pictures/fc7fd407b594d903b778a4c372978c15.png)
![3*[log5 + 1]<p*log5<4*[log5 + 1] 3*[log5 + 1]<p*log5<4*[log5 + 1]](/latexrender/pictures/b83b78a0a62b7b5b95118989eda877d4.png)
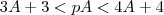 (A = log5)
(A = log5)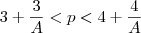
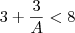 e
e 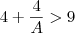


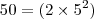
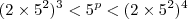
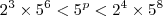

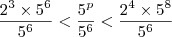
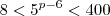
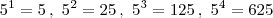
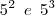 estão entre 8 e 400.
estão entre 8 e 400.

