-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Abr 18, 2013 20:12
por e8group » Qui Abr 18, 2013 20:12
Vamos ver o que acontece se somarmos as duas equações :
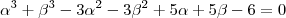
.
Além disso ,como
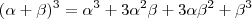
, obtemos que
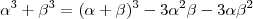
.Assim ,
a equação
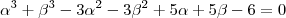
é equivalente a
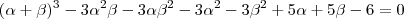
.
ou ainda
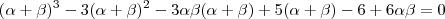
.
Assim , o valor de

corresponde a raiz do polinômio
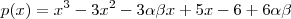
.
Mas ,
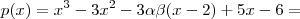
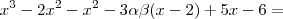
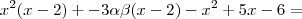
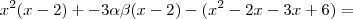
![x^2(x-2) + -3\alpha\beta(x-2) -(x[x -2] -3[x - 2]) = x^2(x-2) + -3\alpha\beta(x-2) -(x[x -2] -3[x - 2]) =](/latexrender/pictures/3703136bafc1cf0049a8fefa7a0fbb9f.png)
Deixando

em evidência ,segue
![p(x) =(x-2)(x^2 -3\alpha \beta -[x-3]) p(x) =(x-2)(x^2 -3\alpha \beta -[x-3])](/latexrender/pictures/6faf530032ba7def17936a458b14c6f6.png)
.
Assim ,
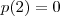
; logo
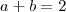
.
Há de ter outra forma também de se resolver este exercício, talvez até seja mais simples .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Qui Abr 18, 2013 22:49
por chronoss » Qui Abr 18, 2013 22:49
Obrigado santhiago , e bela resolução.
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [IMO (Olimpíada In. de Mate.)] 1959 - Q. 1
por raimundoocjr » Qui Fev 14, 2013 14:52
- 2 Respostas
- 731 Exibições
- Última mensagem por raimundoocjr

Sex Fev 15, 2013 22:36
Álgebra Elementar
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8928 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3262 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8830 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2549 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
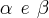 satisfazem as equações :
satisfazem as equações : 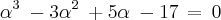
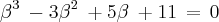


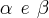 satisfazem as equações :
satisfazem as equações : 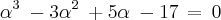
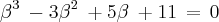


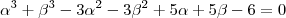 .
.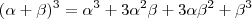 , obtemos que
, obtemos que 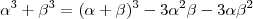 .Assim ,
.Assim ,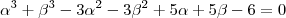 é equivalente a
é equivalente a 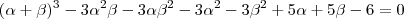 .
. 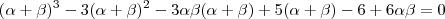 .
.  corresponde a raiz do polinômio
corresponde a raiz do polinômio 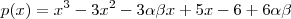 .
.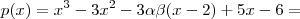
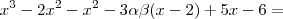
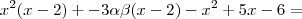
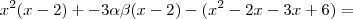
![x^2(x-2) + -3\alpha\beta(x-2) -(x[x -2] -3[x - 2]) = x^2(x-2) + -3\alpha\beta(x-2) -(x[x -2] -3[x - 2]) =](/latexrender/pictures/3703136bafc1cf0049a8fefa7a0fbb9f.png)
 em evidência ,segue
em evidência ,segue ![p(x) =(x-2)(x^2 -3\alpha \beta -[x-3]) p(x) =(x-2)(x^2 -3\alpha \beta -[x-3])](/latexrender/pictures/6faf530032ba7def17936a458b14c6f6.png) .
. 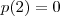 ; logo
; logo 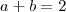 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.