 por replay » Dom Mar 17, 2013 12:22
por replay » Dom Mar 17, 2013 12:22
Dado que a -b = 5 e ab = 2, obtenha o valor numérico de:
b)

Eu fiz assim:
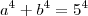
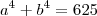
Não sei desenvolver a partir daqui, não há consigo ver a propriedade de:

- Não existe em nenhum livro que eu tenho eu acho.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Mar 17, 2013 15:05
por Russman » Dom Mar 17, 2013 15:05
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INDUÇÃO | DIVISIBILIDADE] ñ consigo iniciar essa questão
por juliohenriquelima14 » Sáb Dez 13, 2014 19:03
- 3 Respostas
- 3149 Exibições
- Última mensagem por juliohenriquelima14

Sáb Dez 13, 2014 23:27
Funções
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8923 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- EXCLUIR CONTA
por Thiago Ramos » Dom Mai 13, 2012 22:38
- 0 Respostas
- 1424 Exibições
- Última mensagem por Thiago Ramos

Dom Mai 13, 2012 22:38
Álgebra Elementar
-
- Urgentissimo (problema com uma conta)
por Misao » Qua Jul 15, 2009 12:52
- 2 Respostas
- 2071 Exibições
- Última mensagem por Misao

Qua Jul 15, 2009 16:17
Progressões
-
- Função - Problema na conta
por guijermous » Ter Fev 16, 2010 11:05
- 5 Respostas
- 4709 Exibições
- Última mensagem por MarceloFantini

Ter Fev 16, 2010 12:03
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

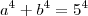
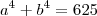
 - Não existe em nenhum livro que eu tenho eu acho.
- Não existe em nenhum livro que eu tenho eu acho.

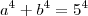
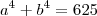
 - Não existe em nenhum livro que eu tenho eu acho.
- Não existe em nenhum livro que eu tenho eu acho.

