 por Janffs » Seg Dez 24, 2012 01:07
por Janffs » Seg Dez 24, 2012 01:07
Se a expressão
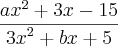
independe de x, com a e b reais, então a + b vale
A) -4
B) -6
C) -8
D) -10
E) -12
A solução da equação
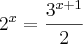
é
A)
![\left[log\frac{1}{10} \right] \left[log\frac{1}{10} \right]](/latexrender/pictures/ef995d0821e8f981e7cb5bbcd76d73c0.png)
B)
![\left[log\frac{1}{20} \right] \left[log\frac{1}{20} \right]](/latexrender/pictures/5f9dfa7381b392da373415e274c9c0b9.png)
C)
![\left[log\frac{1}{30} \right] \left[log\frac{1}{30} \right]](/latexrender/pictures/658aa4e990e1cf774bfb61401fd6a87d.png)
D)
![\left[log\frac{3}{2} \right] \left[log\frac{3}{2} \right]](/latexrender/pictures/34fdc31cc7d05decbc136334f8474b02.png)
E)
![\left[log\frac{2}{3} \right] \left[log\frac{2}{3} \right]](/latexrender/pictures/ff01d25f1a6f58bad35c88bc63782bd9.png)
Se
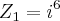
e
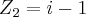
, onde
![i=\sqrt[]{-1} i=\sqrt[]{-1}](/latexrender/pictures/7dc91cc10f3c198f0d5943cc25d7dc57.png)
, então o módulo de
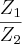
é igual a:
A)

B)
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)
C)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
D)
![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png)
E)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Será que alguem me ajuda por favor........
-
Janffs
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Nov 15, 2012 16:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Seg Dez 24, 2012 11:30
por e8group » Seg Dez 24, 2012 11:30
Dada uma função

, ela é dita "independente de x " quando ela é constante,isto é ,qualquer valor real que

assumir temos que o resultado de

é o mesmo .
Vamos supor que
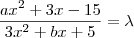
.
Onde :

é uma constante real para qualquer

real .
Agora multiplicando ambos lados por
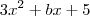
(Claro que (
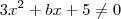
)segue ,

.
Perceba que esta igualdade de polinômios só será verdadeira quando os seus respectivos coeficientes forem iguais . Portanto ,
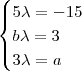
.
Tente concluir ....
No segundo exercício ,note que:

.
Ora , se as bases são diferentes e seus repectivos expoentes são iguais . Quando esta igualdade é verdadeira ? Qual o valor que

deve assumir ?
OBS.: Próxima vez post apenas um exercício por tópico ,além disso seria muito importante expor sua dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ifba
por zenildo » Ter Set 24, 2013 15:07
- 1 Respostas
- 2655 Exibições
- Última mensagem por DanielFerreira

Qui Fev 20, 2014 18:22
Conjuntos
-
- [Lógica e Noções de Álgebra de Boole ] 4 questões
 por designeredpascoal » Qua Ago 01, 2018 18:09
por designeredpascoal » Qua Ago 01, 2018 18:09
- 0 Respostas
- 3013 Exibições
- Última mensagem por designeredpascoal

Qua Ago 01, 2018 18:09
Lógica
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2593 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- Números primos e outras travas
por victorleme » Ter Mai 03, 2011 11:20
- 5 Respostas
- 4427 Exibições
- Última mensagem por victorleme

Qua Mai 04, 2011 00:54
Álgebra Elementar
-
- [Função Modular] Outras perspectivas
por Jhenrique » Qui Set 13, 2012 02:50
- 1 Respostas
- 996 Exibições
- Última mensagem por MarceloFantini

Qui Set 13, 2012 10:05
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
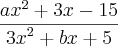 independe de x, com a e b reais, então a + b vale
independe de x, com a e b reais, então a + b vale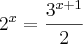 é
é![\left[log\frac{1}{10} \right] \left[log\frac{1}{10} \right]](/latexrender/pictures/ef995d0821e8f981e7cb5bbcd76d73c0.png)
![\left[log\frac{1}{20} \right] \left[log\frac{1}{20} \right]](/latexrender/pictures/5f9dfa7381b392da373415e274c9c0b9.png)
![\left[log\frac{1}{30} \right] \left[log\frac{1}{30} \right]](/latexrender/pictures/658aa4e990e1cf774bfb61401fd6a87d.png)
![\left[log\frac{3}{2} \right] \left[log\frac{3}{2} \right]](/latexrender/pictures/34fdc31cc7d05decbc136334f8474b02.png)
![\left[log\frac{2}{3} \right] \left[log\frac{2}{3} \right]](/latexrender/pictures/ff01d25f1a6f58bad35c88bc63782bd9.png)
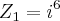 e
e 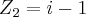 , onde
, onde ![i=\sqrt[]{-1} i=\sqrt[]{-1}](/latexrender/pictures/7dc91cc10f3c198f0d5943cc25d7dc57.png) , então o módulo de
, então o módulo de 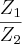 é igual a:
é igual a:
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)

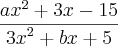 independe de x, com a e b reais, então a + b vale
independe de x, com a e b reais, então a + b vale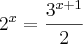 é
é![\left[log\frac{1}{10} \right] \left[log\frac{1}{10} \right]](/latexrender/pictures/ef995d0821e8f981e7cb5bbcd76d73c0.png)
![\left[log\frac{1}{20} \right] \left[log\frac{1}{20} \right]](/latexrender/pictures/5f9dfa7381b392da373415e274c9c0b9.png)
![\left[log\frac{1}{30} \right] \left[log\frac{1}{30} \right]](/latexrender/pictures/658aa4e990e1cf774bfb61401fd6a87d.png)
![\left[log\frac{3}{2} \right] \left[log\frac{3}{2} \right]](/latexrender/pictures/34fdc31cc7d05decbc136334f8474b02.png)
![\left[log\frac{2}{3} \right] \left[log\frac{2}{3} \right]](/latexrender/pictures/ff01d25f1a6f58bad35c88bc63782bd9.png)
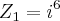 e
e 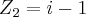 , onde
, onde ![i=\sqrt[]{-1} i=\sqrt[]{-1}](/latexrender/pictures/7dc91cc10f3c198f0d5943cc25d7dc57.png) , então o módulo de
, então o módulo de 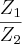 é igual a:
é igual a:
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)

 , ela é dita "independente de x " quando ela é constante,isto é ,qualquer valor real que
, ela é dita "independente de x " quando ela é constante,isto é ,qualquer valor real que  assumir temos que o resultado de
assumir temos que o resultado de  é o mesmo .
é o mesmo . 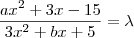 .
.  é uma constante real para qualquer
é uma constante real para qualquer  real .
real . 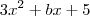 (Claro que (
(Claro que (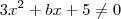 )segue ,
)segue ,  .
. 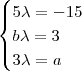 .
.  .
.  deve assumir ?
deve assumir ? 
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.