 por rodrigonapoleao » Seg Nov 19, 2012 16:28
por rodrigonapoleao » Seg Nov 19, 2012 16:28
como acho a soluçao do conjunto |x-1|>|x|?
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 23:25
por MarceloFantini » Seg Nov 19, 2012 23:25
Primeiro, não existe solução de um conjunto. Neste caso é o
conjunto solução da inequação.
Para resolvê-la, precisa considerar os casos

No primeiro teremos

.
No segundo teremos

.
No terceiro teremos

Note então que no primeiro caso não existe solução, pois -1 é menor, e não maior, que zero. Logo não existem soluções maiores ou iguais a um.
No segundo caso encontramos que

e

. Como
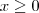
, segue que a solução será

.
Por último, sabemos que

sempre, logo todo
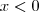
é solução.
Unindo as respostas chegamos em

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
. .
.
 e
e  . Como
. Como 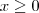 , segue que a solução será
, segue que a solução será  .
. sempre, logo todo
sempre, logo todo 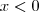 é solução.
é solução. .
.

