 por SCHOOLGIRL+T » Qua Nov 07, 2012 20:39
por SCHOOLGIRL+T » Qua Nov 07, 2012 20:39
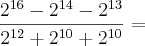
Me ajudem a simplificar?
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Nov 07, 2012 21:00
por Russman » Qua Nov 07, 2012 21:00
Lembre-se que
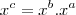
se
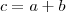
. Ou seja,
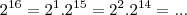
Portanto basta que você observe a menor potência e a fatore. Exemplo,
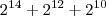
Veja que

é a menor potência, que
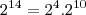
e
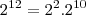
. Portanto,
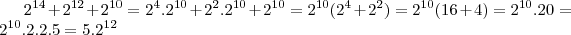
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por SCHOOLGIRL+T » Qui Nov 08, 2012 19:56
por SCHOOLGIRL+T » Qui Nov 08, 2012 19:56
Russman escreveu:Lembre-se que
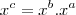
se
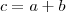
. Ou seja,
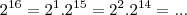
Portanto basta que você observe a menor potência e a fatore. Exemplo,
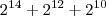
Veja que

é a menor potência, que
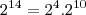
e
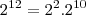
. Portanto,
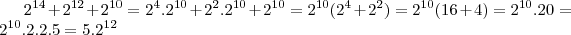
Obrigada^^
Me ajudo bastante.
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2292 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1739 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3745 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2025 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- POTENCIACAO
por CaAtr » Ter Mar 09, 2010 20:23
- 3 Respostas
- 2294 Exibições
- Última mensagem por CaAtr

Ter Mar 09, 2010 22:17
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
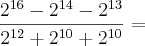

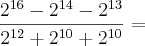

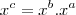 se
se 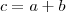 . Ou seja,
. Ou seja,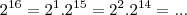
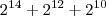
 é a menor potência, que
é a menor potência, que 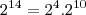 e
e 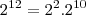 . Portanto,
. Portanto,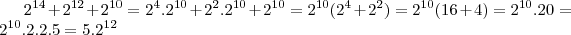

se
. Ou seja,
é a menor potência, que
e
. Portanto,


 .
.



