(Olimpíada de Matemática) O valor de
 .
. .
. .
. é :
é :Então, eu fiz assim:
 .
. .
. .
.
Como a ordem dos fatores não altera o produto.
 .
. .
. .
. =
= .
. .
. .
. =
==
 .
.
Parei ai. Não consegui resolver o restante.

 .
. .
. .
. é :
é : .
. .
. .
.
 .
. .
. .
. =
= .
. .
. .
. =
= .
.

Bielto escreveu:Bom, pra não dizerem que eu não tentei, eu fiz até onde deu
(Olimpíada de Matemática) O valor de.
.
.
é :
Então, eu fiz assim:.
.
.
Como a ordem dos fatores não altera o produto..
.
.
=
.
.
.
=
=.
Parei ai. Não consegui resolver o restante.



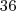




 , por isso não continuei com o raciocínio.
, por isso não continuei com o raciocínio. não era pra dar
não era pra dar  ?
? ? Não entendi, a única propriedade que eu conheço nesse caso para resolver é a
? Não entendi, a única propriedade que eu conheço nesse caso para resolver é a 
 .
. 
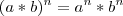

Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes