 por Luiz Junior » Seg Jun 18, 2012 19:45
por Luiz Junior » Seg Jun 18, 2012 19:45
Peço a ajuda para que alguém habilitado resolva o exercício abaixo para mim por gentileza.
Prove que: 2.1 + 2.2 + 2.3 + . . . + 2 n = n² + n, para n ? 1.
1)passo base: (eu consegui fazer)
P(1) = 2.1+2.2+2.3+...+2.1= +1=2, é verdadeiro para n=1
+1=2, é verdadeiro para n=1
2) passo indutivo:
Para n= k, teremos: 2.1 + 2. 2 + 2.3 + . . . + 2k = k² + k, k ? 1
Deve-se mostrar que: 2 .1 +2.2 + 2.3 + . . . + 2k + 2 ( k + 1)= ( k² +1 )² + k + 1
Continue a demonstração.....
Daqui pra frente que não consigo fazer!Desde já agradeço pela atenção e colaboração.
-
Luiz Junior
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jun 18, 2012 19:41
- Formação Escolar: SUPLETIVO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por MarceloFantini » Seg Jun 18, 2012 23:32
por MarceloFantini » Seg Jun 18, 2012 23:32
Bastava perceber que

.
Continuando da sua demonstração, note que

que por hipótese temos

, daí

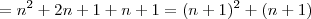
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Luiz Junior » Ter Jun 19, 2012 12:49
por Luiz Junior » Ter Jun 19, 2012 12:49
Fico grato Marcelo Fantini.
Vlw pela explicação... Passando a entender Indução!
Abraço!
-
Luiz Junior
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jun 18, 2012 19:41
- Formação Escolar: SUPLETIVO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2687 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3069 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
-
- Indução Matemática
por Abelardo » Qui Mar 31, 2011 03:04
- 1 Respostas
- 2538 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:27
Álgebra Elementar
-
- Indução matemática
por TiagoFERD » Dom Mar 04, 2012 10:08
- 6 Respostas
- 4505 Exibições
- Última mensagem por TiagoFERD

Seg Mar 05, 2012 18:55
Progressões
-
- Indução Matemática
por MateusDantas1 » Dom Mar 04, 2012 13:00
- 1 Respostas
- 1726 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 01:50
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 +1=2, é verdadeiro para n=1
+1=2, é verdadeiro para n=1

 .
. que por hipótese temos
que por hipótese temos  , daí
, daí
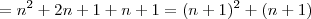 .
.


 .
.



