 por jvabatista » Qua Abr 18, 2012 02:05
por jvabatista » Qua Abr 18, 2012 02:05
Olá.
Eu resolvi a equação

colocando tudo que não tem módulo no 1º membro, ficando:
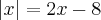
.
Em seguida, transformei a equação em duas:
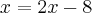
e

, encontrando como resultado 8 e 8/3 respectivamente. Mas na resposta do livro só aparece como resposta o 8 e quando substitui 8/3 na equação realmente vê que ele não serve. Por que isso acontece? Tem algo errado na forma como resolvi ?
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por jacobi » Qua Abr 18, 2012 10:46
por jacobi » Qua Abr 18, 2012 10:46
jvabatista escreveu:Olá.
Eu resolvi a equação

colocando tudo que não tem módulo no 1º membro, ficando:
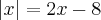
.
Em seguida, transformei a equação em duas:
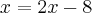
e

, encontrando como resultado 8 e 8/3 respectivamente. Mas na resposta do livro só aparece como resposta o 8 e quando substitui 8/3 na equação realmente vê que ele não serve. Por que isso acontece? Tem algo errado na forma como resolvi ?
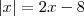
Se
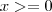
, entao

. Daí,

;

. Realmente,
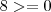
. Essa vale.
Se
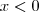
, entao
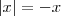
. Daí,
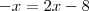
;
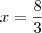
. Porém

nao é menor que

, por isso, nao vale.
-
jacobi
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Abr 18, 2012 10:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Aluno
- Andamento: cursando
 por jvabatista » Qua Abr 25, 2012 23:22
por jvabatista » Qua Abr 25, 2012 23:22
Muito obrigado pelo esclarecimento. Breve, estarei mandando outras dúvidas que me surgirem. Abraços.
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calcular XV dessa equação] ( Confuso !! )
por Andre Lopes » Sex Ago 30, 2013 13:08
- 0 Respostas
- 1070 Exibições
- Última mensagem por Andre Lopes

Sex Ago 30, 2013 13:08
Funções
-
- Equação com fração, resultado sem nexo.
por Matheus Lacombe O » Sex Fev 24, 2012 11:23
- 2 Respostas
- 1854 Exibições
- Última mensagem por Neperiano

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3418 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação modular
por amandactdas » Qui Jul 23, 2009 13:14
- 1 Respostas
- 2800 Exibições
- Última mensagem por Molina

Qui Jul 23, 2009 15:26
Funções
-
- Equação modular.
por JoaoGabriel » Sáb Set 18, 2010 11:01
- 3 Respostas
- 2514 Exibições
- Última mensagem por JoaoGabriel

Sáb Set 18, 2010 14:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 colocando tudo que não tem módulo no 1º membro, ficando:
colocando tudo que não tem módulo no 1º membro, ficando: 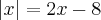 .
.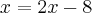 e
e  , encontrando como resultado 8 e 8/3 respectivamente. Mas na resposta do livro só aparece como resposta o 8 e quando substitui 8/3 na equação realmente vê que ele não serve. Por que isso acontece? Tem algo errado na forma como resolvi ?
, encontrando como resultado 8 e 8/3 respectivamente. Mas na resposta do livro só aparece como resposta o 8 e quando substitui 8/3 na equação realmente vê que ele não serve. Por que isso acontece? Tem algo errado na forma como resolvi ?

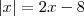
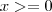 , entao
, entao  . Daí,
. Daí,  ;
;  . Realmente,
. Realmente, 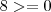 . Essa vale.
. Essa vale.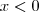 , entao
, entao 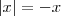 . Daí,
. Daí, 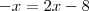 ;
; 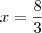 . Porém
. Porém  nao é menor que
nao é menor que  , por isso, nao vale.
, por isso, nao vale.

 .
.



