A afirmação é esta
Se a é par e não é quadrado perfeito
![\Rightarrow \sqrt[]{a} \Rightarrow \sqrt[]{a}](/latexrender/pictures/237d4b1ac1f3ac5c9b00292f46d0efdc.png) é irracional
é irracionalObrigado.

![\Rightarrow \sqrt[]{a} \Rightarrow \sqrt[]{a}](/latexrender/pictures/237d4b1ac1f3ac5c9b00292f46d0efdc.png) é irracional
é irracional
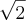 é irracional, vejam se vocês concordam:
é irracional, vejam se vocês concordam: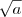 é racional, isto é
é racional, isto é 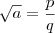
 e
e  inteiros positivos,
inteiros positivos,  ,
,  e
e  primos entre si.
primos entre si. é par, seja
é par, seja 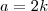 ,
,  um número primo. Então
um número primo. Então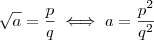 ,
, 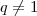 pois
pois  não é quadrado perfeito,
não é quadrado perfeito, então 2 divide
então 2 divide 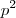 logo 2 divide
logo 2 divide  .
.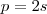 , então
, então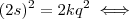

 , pois assumimos
, pois assumimos  sendo um número primo. Então 2 deve dividir
sendo um número primo. Então 2 deve dividir 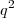 e portanto 2 divide
e portanto 2 divide  .
. e 2 é um fator de
e 2 é um fator de  . Dessa forma
. Dessa forma  e
e  não são primos entre si, o que contradiz a nossa hipótese.
não são primos entre si, o que contradiz a nossa hipótese.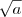 é irracional.
é irracional.

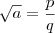 sendo que
sendo que  é um número racional na forma de fração irredutível e portanto
é um número racional na forma de fração irredutível e portanto  é mínimo (o menor valor que satisfaz essa igualdade).
é mínimo (o menor valor que satisfaz essa igualdade).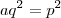 .
. é par então
é par então 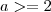 , então
, então 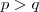 e
e  senão
senão  seria um quadrado perfeito.
seria um quadrado perfeito. temos
temos  .
. , onde
, onde  é o resto da divisão euclidiana,
é o resto da divisão euclidiana, 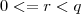
 então
então  é um quadrado perfeito logo
é um quadrado perfeito logo 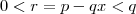 .
.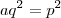 então
então então
então então
então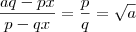 .
.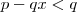 , temos uma contradição à nossa hipótese de que
, temos uma contradição à nossa hipótese de que  é mímimo.
é mímimo.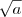 é irracional.
é irracional.
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.