Olá pessoal, tudo bem?
Sou programador e estou precisando montar uma formula para descobrir se há intersecção entre conjuntos.
Na verdade, meu sistema controla atividades por período de meses.
Logo um funcionário não pode ter mais de uma atividade por período.
Sendo assim, se um "João" esta no "setor de manutenção" de "Janeiro a Junho", o sistema não pode deixar cadastrar o "setor de limpeza" no período de "Março a Agosto", pois há uma intersecção de meses ("Março a Junho").
Sendo assim, qual a formula que me diz se há intersecção entre dois conjuntos?


 .Neste caso diz-se que os conjuntos são disjuntos.
.Neste caso diz-se que os conjuntos são disjuntos.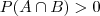 .
.