 por Pri Ferreira » Qua Mar 21, 2012 13:11
por Pri Ferreira » Qua Mar 21, 2012 13:11
Desenvolvendo-se a expressão 4^60 x 5^113, obtém-se um
número inteiro n, cuja soma dos algarismos corresponde a:
(A) 9
(B) 10
(C) 11
(D) 12
Questão de concurso que gostaria muito de ver a resolução!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por LuizAquino » Qua Mar 21, 2012 20:36
por LuizAquino » Qua Mar 21, 2012 20:36
Pri Ferreira escreveu:Desenvolvendo-se a expressão 4^60 x 5^113, obtém-se um
número inteiro n, cuja soma dos algarismos corresponde a:
(A) 9
(B) 10
(C) 11
(D) 12
Pri Ferreira escreveu:Questão de concurso que gostaria muito de ver a resolução!!
Note que:
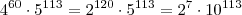
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Pri Ferreira » Qui Mar 22, 2012 01:24
por Pri Ferreira » Qui Mar 22, 2012 01:24
Olá muito obrigada pela ajuda!!!
Mas ainda naum entendi esse passo...
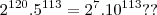
Pode explicar melhor?? Obrigada!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por DanielFerreira » Qui Mar 22, 2012 01:31
por DanielFerreira » Qui Mar 22, 2012 01:31
Pri Ferreira escreveu:Olá muito obrigada pela ajuda!!!
Mas ainda naum entendi esse passo...
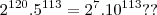
Pode explicar melhor?? Obrigada!!!
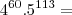

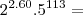
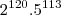
(...)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Pri Ferreira » Dom Mar 25, 2012 18:22
por Pri Ferreira » Dom Mar 25, 2012 18:22
Agora entendi!!!
Obrigada!!
Consegui terminar!!
Mt obrigada msm pela ajuda!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Expressão
por geriane » Qui Abr 22, 2010 12:49
- 4 Respostas
- 3893 Exibições
- Última mensagem por geriane

Sáb Abr 24, 2010 10:50
Trigonometria
-
- Expressão em PG
por Carolziiinhaaah » Qua Jun 16, 2010 21:10
- 1 Respostas
- 2009 Exibições
- Última mensagem por MarceloFantini

Qua Jun 16, 2010 21:39
Progressões
-
- EXPRESSAO
 por JOHNY » Dom Set 05, 2010 15:26
por JOHNY » Dom Set 05, 2010 15:26
- 1 Respostas
- 2094 Exibições
- Última mensagem por MarceloFantini

Seg Set 06, 2010 13:14
Álgebra Elementar
-
- expressão
por jose henrique » Qua Fev 16, 2011 18:16
- 11 Respostas
- 7749 Exibições
- Última mensagem por jose henrique

Seg Fev 28, 2011 19:39
Álgebra Elementar
-
- Expressão
por maria cleide » Dom Mai 08, 2011 16:47
- 1 Respostas
- 1813 Exibições
- Última mensagem por Molina

Dom Mai 08, 2011 18:01
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



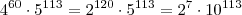

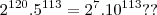

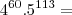

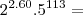
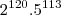

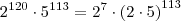




 , avisa que eu resolvo.
, avisa que eu resolvo.

