 por nathyn » Qui Mar 01, 2012 10:47
por nathyn » Qui Mar 01, 2012 10:47
Oie gente, eu estou tentando aprender log com o livro fundamentos 2, mas até chegar a parte de log tenho um longo caminho, e ainda me prendo muito em algumas questões que não consigo fazer =/.
Por favor me ajudem!! Segue as questões...
1-)Se na expressão
![\frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3} \frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3}](/latexrender/pictures/5777bacbd014308102cfb07be412cdfa.png)
, com x >8, substituirmos
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
por t, obteremos a expressão equivalente a:
a)
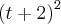
b)
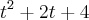
c)
![\sqrt[]{\left(7 + t \right)}+ 3 \sqrt[]{\left(7 + t \right)}+ 3](/latexrender/pictures/8fc2349a2deb23789c73b4d03c38c21c.png)
d)
![\frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}} \frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}}](/latexrender/pictures/abd3efc8de75ff4a1306fbe4ac51395a.png)
e)
![\left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right] \left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right]](/latexrender/pictures/e1a3e00fc17f7bbe10b71827119cdc5b.png)
Resp: E
Eu troquei
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
por t e Racionalizei o denominador ficando...
![\frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3} \frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3}](/latexrender/pictures/d307d8081997b5dd52db5dd2d91cff6e.png)
![\frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2} \frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2}](/latexrender/pictures/39ed4e4951805ba41b5701959bde6021.png)
Daí em diante não sei mas como fazer =/
Me ajude por favor! =/
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qui Mar 01, 2012 23:44
por DanielFerreira » Qui Mar 01, 2012 23:44
nathyn escreveu:Oie gente, eu estou tentando aprender log com o livro fundamentos 2, mas até chegar a parte de log tenho um longo caminho, e ainda me prendo muito em algumas questões que não consigo fazer =/.
Por favor me ajudem!! Segue as questões...
1-)Se na expressão
![\frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3} \frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3}](/latexrender/pictures/5777bacbd014308102cfb07be412cdfa.png)
, com x >8, substituirmos
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
por t, obteremos a expressão equivalente a:
a)
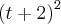
b)
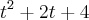
c)
![\sqrt[]{\left(7 + t \right)}+ 3 \sqrt[]{\left(7 + t \right)}+ 3](/latexrender/pictures/8fc2349a2deb23789c73b4d03c38c21c.png)
d)
![\frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}} \frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}}](/latexrender/pictures/abd3efc8de75ff4a1306fbe4ac51395a.png)
e)
![\left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right] \left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right]](/latexrender/pictures/e1a3e00fc17f7bbe10b71827119cdc5b.png)
Resp: E
Eu troquei
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
por t e Racionalizei o denominador ficando...
![\frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3} \frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3}](/latexrender/pictures/d307d8081997b5dd52db5dd2d91cff6e.png)
![\frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2} \frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2}](/latexrender/pictures/39ed4e4951805ba41b5701959bde6021.png)
Daí em diante não sei mas como fazer =/
Me ajude por favor! =/
Nathyn,
faltou apenas você ter fatorado (t³ - 8) e simplificar, veja:
(a³ - b³) = (a - b)(a² + ab + b²)
(t³ - 8) = (t³ - 2³)
(t³ - 2³) = (t - 2)(t² + 2t + 4)
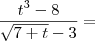
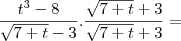
![\frac{(t - 2)(t^2 + 2t + 4)[\sqrt{7 + t} + 3]}{(7 + t) - 9} = \frac{(t - 2)(t^2 + 2t + 4)[\sqrt{7 + t} + 3]}{(7 + t) - 9} =](/latexrender/pictures/cebb8accb70176d897f3ba2ec2100186.png)
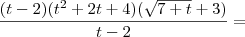
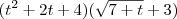
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por nathyn » Qua Mar 21, 2012 16:05
por nathyn » Qua Mar 21, 2012 16:05
Entendi direitinho,
brigadão! ,D
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2841 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2829 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2242 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2193 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3} \frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3}](/latexrender/pictures/5777bacbd014308102cfb07be412cdfa.png) , com x >8, substituirmos
, com x >8, substituirmos ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) por t, obteremos a expressão equivalente a:
por t, obteremos a expressão equivalente a: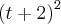
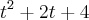
![\sqrt[]{\left(7 + t \right)}+ 3 \sqrt[]{\left(7 + t \right)}+ 3](/latexrender/pictures/8fc2349a2deb23789c73b4d03c38c21c.png)
![\frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}} \frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}}](/latexrender/pictures/abd3efc8de75ff4a1306fbe4ac51395a.png)
![\left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right] \left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right]](/latexrender/pictures/e1a3e00fc17f7bbe10b71827119cdc5b.png)
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) por t e Racionalizei o denominador ficando...
por t e Racionalizei o denominador ficando...![\frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3} \frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3}](/latexrender/pictures/d307d8081997b5dd52db5dd2d91cff6e.png)
![\frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2} \frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2}](/latexrender/pictures/39ed4e4951805ba41b5701959bde6021.png)


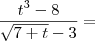
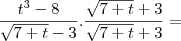
![\frac{(t - 2)(t^2 + 2t + 4)[\sqrt{7 + t} + 3]}{(7 + t) - 9} = \frac{(t - 2)(t^2 + 2t + 4)[\sqrt{7 + t} + 3]}{(7 + t) - 9} =](/latexrender/pictures/cebb8accb70176d897f3ba2ec2100186.png)
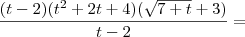
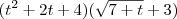

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.