 por timoteo » Sáb Fev 18, 2012 13:07
por timoteo » Sáb Fev 18, 2012 13:07
bem, esse problema foi criado por Fermat e ja foi provado pelo sr. Wiles, matematico britanico, mais de 300 anos depois de sua publicaçao. olhem o google.
eu li sobre ele ha uns dois anos e fiquei interessado em tentar resolve-lo. pensei nele por meses sem nem colocar no papel e em uma bela noite algo me sucedeu.
nao sou um matematico, ainda, entao nao consigo concluir a prova ou sequer notar as falhas, pois estou maravilhado com a simplicidade da resposta. gostaria que vcs me ajudassem a ver algum erro ou partes confusas.
o enunciado do teorema diz: Que não há solução para a equação
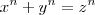
, se n for um inteiro maior do que 2 e x, y e z naturais (inteiros > 0).
1° parte.
o enunciado diz inteiros positivos, entao sendo (a+1) a razao dos inteiros, com a > 0.
agora utilizando o binomio de Newton temos:

para todo n

0.
desenvolvendo o binomio:

=
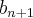

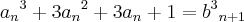
...
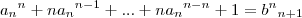
2° parte.
como podemos ver o monomio
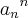
do primeiro termo é o antecessor de
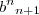
; esses dois termos sao valores consecutivos em uma sequencia que denominaremos de Pn para cada valor de n. sendo assim teremos para cada numero natural um conjunto de grau n.
ex: P2= { 4, 9, 16...}; para cada valor natural existe um valor de grau n=2.
para encontrar dois termos consecutivos na sequencia Pn é so colocar um numero natural em
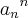
e com isso obteremos o seu sucessor
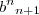
.
3° parte.
fazendo o sucessor menos o antecessor teremos o valor

que é a distancia entre os termos.
se observarmos as sequencias polinomiais da 1° parte perceberemos que a distancia entre os termos de grau maior n > 2 sao formados pela soma de monomios que tem expoentes n

2.
o que quero provar é que o fato de a distancia entre o antecessor e sucessor é dado por um polinomio de grau n

2. isso para mim gera uma proporçao nao direta, diferente do que ocorre nos casos triviais de n=1 e n=2 onde a distancia é um proporçao direta formada por uma funçao linear.
eu imagino que o fato de em n=2 a formula da distancia
![{D}_{} = \sqrt[]{{(x - x)}^{2} + {(y - y)}^{2}} {D}_{} = \sqrt[]{{(x - x)}^{2} + {(y - y)}^{2}}](/latexrender/pictures/813b779a606d9244692f21c93880efed.png)
ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes n

3 nao tem soluçao. isso prova o ultimo teorema de Fermat.
Obs. hoje acreditam que Fermat errou ao fazer a prova, pois Sr. Wiles somente consegui a resposta utilizando matematica que nao existia no tempo de Fermat. caso essa logica esteja certa, ela pode se aproximar da resposta da epoca de Fermat.
antecipadamente agradeço as criticas construtivas.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por LuizAquino » Sáb Fev 18, 2012 17:08
por LuizAquino » Sáb Fev 18, 2012 17:08
timoteo escreveu:1° parte.
o enunciado diz inteiros positivos, entao sendo (a+1) a razao dos inteiros, com a > 0.
agora utilizando o binomio de Newton temos:

para todo

.
desenvolvendo o binomio:
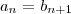

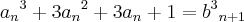
...
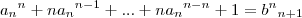
A notação
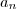
e
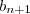
ficou confusa. Mas ao que parece, você deseja dizer que o número inteiro
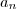
é antecessor do número inteiro
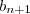
. Ou seja, que temos:

Em seguida, você deseja elevar ambos os membros dessa equação por um certo número inteiro positivo e não nulo. No final do processo, você decidiu usar a letra n para representar esse número. Entretanto, isso gera confusão com a letra n que você já usou para indicar que
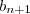
é sucessor de
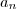
. Nesse contexto, vale a pena trocar um desses enes por outra letra. Por exemplo, você poderia usar a letra k em
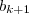
e
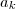
Elevando então por n (sendo n inteiro positivo e não nulo), temos um binômio de Newton:
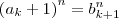
Desenvolvendo o primeiro membro, temos que:

Observação: Note que você escreveu algo como
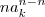
antes do 1, ao invés de
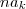
como deveria ser.
timoteo escreveu:2° parte.
como podemos ver o monomio
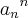
do primeiro termo é o antecessor de
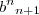
; esses dois termos sao valores consecutivos em uma sequencia que denominaremos de Pn para cada valor de n. sendo assim teremos para cada numero natural um conjunto de grau n.
ex: P2= { 4, 9, 16...}; para cada valor natural existe um valor de grau n=2.
para encontrar dois termos consecutivos na sequencia Pn é so colocar um numero natural em
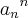
e com isso obteremos o seu sucessor
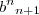
.
Bem, o inteiro
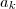
é antecessor de
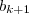
, pois você fez essa suposição no início de sua argumentação.
Entretanto, o inteiro
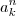
não será antecessor de
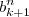
. Por exemplo, 5 é o antecessor de 6, mas 5² não é o antecessor de 6².
Além disso, ao que parece você deseja nessa parte definir a sequência:
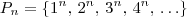
Por exemplo,
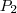
seria
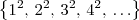
.
Já
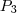
seria

.
E assim por diante.
timoteo escreveu:3° parte.
fazendo o sucessor menos o antecessor teremos o valor

que é a distancia entre os termos.
se observarmos as sequencias polinomiais da 1° parte perceberemos que a distancia entre os termos de grau maior n > 2 sao formados pela soma de monomios que tem expoentes

.
o que quero provar é que o fato de a distancia entre o antecessor e sucessor é dado por um polinomio de grau n \geq 2. isso para mim gera uma proporçao nao direta, diferente do que ocorre nos casos triviais de n=1 e n=2 onde a distancia é um proporçao direta formada por uma funçao linear.
eu imagino que o fato de em n=2 a formula da distancia

ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes

nao tem soluçao. isso prova o ultimo teorema de Fermat.
Vamos representar por
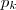
o k-ésimo termo da sequência
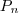
definida anteriormente. Teremos que

.
A diferença entre
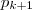
e
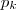
(dois termos consecutivos de
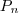
) , será dada por
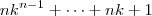
.
A associação que você está argumentando entre essa diferença e o Último Teorema de Fermat não é conclusiva.
Na verdade, o que você está fazendo é tentar analisar um caso particular do teorema, quando z = x + 1 na equação
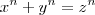
.
Ou seja, é como se você estivesse pensando na seguinte proposição:
Se x e z são dois números naturais consecutivos, então não há solução para a equação
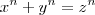
(com n > 2 e y natural).
Observação: a fórmula da distância entre
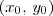
e
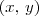
é dada por

. Note que a expressão que você escreveu é na verdade equivalente a
D = 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por timoteo » Sáb Fev 18, 2012 20:26
por timoteo » Sáb Fev 18, 2012 20:26
(nao estou conseguido fazer as citaçoes, algo esta dando errado)
ola Luiz, gostei de seu parecer. sei que cometi alguns erros de escrita, mas é pq sempre acho que todos entenderao o basico, porem sei que essa explicaçao por menorizada é importante. pulando a parte da escrita vamos para as interpretaçoes.
LuizAquino escreveu:A notação e ficou confusa. Mas ao que parece, você deseja dizer que o número inteiro é antecessor do número inteiro . Ou seja, que temos:
. aqui vc entendeu que eu disse que
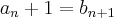
. usando a notaçao que vc indicou, façamos a verdadeira interpretaçao.
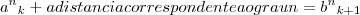
esses dois termos estao contidos na sequencia de grau n.
LuizAquino escreveu:Bem, o inteiro é antecessor de , pois você fez essa suposição no início de sua argumentação.
Entretanto, o inteiro não será antecessor de . Por exemplo, 5 é o antecessor de 6, mas 5² não é o antecessor de 6².
Além disso, ao que parece você deseja nessa parte definir a sequência:
Por exemplo, seria .
Já seria .
acho que para facilitar a compreensao eu deveria dizer que existe um conjunto G que contem todas as sequencias Pn. como vc disse 5 é antecessor de 6 na P1 e na P2 25 é antecessor de 36. é nesse ponto que houve uma confusao pois deixei de dizer que a o polinomio de grau n é uma funçao entre os naturais e os correspondentes de Pn.
seguindo seu raciocinio temos 5 é antecessor de 6 nos naturais e 25 é sucessor de 36 na sequencia de grau 2. seguindo o mesmo raciocinio desenvolvemos os termos de cada sequencia Pn. ex= em P3= {
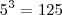
antecessor
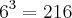
sucessor}.
bem, acho que da para tirar algumas duvidas Luiz.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teorema de Fermat] Problema
por dravz » Seg Fev 25, 2013 01:55
- 1 Respostas
- 1011 Exibições
- Última mensagem por Russman

Seg Fev 25, 2013 03:15
Cálculo: Limites, Derivadas e Integrais
-
- Ultimo simulado
por Guilherme35 » Seg Set 17, 2012 02:15
- 1 Respostas
- 1174 Exibições
- Última mensagem por MarceloFantini

Seg Set 17, 2012 17:54
Álgebra Elementar
-
- [Google] Homenagem a Fermat
 por Molina » Qua Ago 17, 2011 20:10
por Molina » Qua Ago 17, 2011 20:10
- 2 Respostas
- 2138 Exibições
- Última mensagem por MarceloFantini

Sex Ago 19, 2011 20:26
Assuntos Gerais ou OFF-TOPIC
-
- Módulo de número complexo ( questão do último concurso )
por Andreza » Sáb Out 22, 2011 11:23
- 1 Respostas
- 1846 Exibições
- Última mensagem por MarceloFantini

Sáb Out 22, 2011 15:21
Números Complexos
-
- Teorema das linhas
por valleska » Seg Mai 18, 2009 21:46
- 1 Respostas
- 3264 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 11:20
Desafios Enviados
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
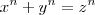 , se n for um inteiro maior do que 2 e x, y e z naturais (inteiros > 0).
, se n for um inteiro maior do que 2 e x, y e z naturais (inteiros > 0). para todo n
para todo n  0.
0. =
= 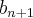

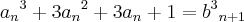
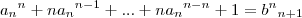
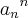 do primeiro termo é o antecessor de
do primeiro termo é o antecessor de 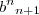 ; esses dois termos sao valores consecutivos em uma sequencia que denominaremos de Pn para cada valor de n. sendo assim teremos para cada numero natural um conjunto de grau n.
; esses dois termos sao valores consecutivos em uma sequencia que denominaremos de Pn para cada valor de n. sendo assim teremos para cada numero natural um conjunto de grau n. 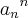 e com isso obteremos o seu sucessor
e com isso obteremos o seu sucessor 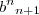 .
. que é a distancia entre os termos.
que é a distancia entre os termos. 2.
2. 2. isso para mim gera uma proporçao nao direta, diferente do que ocorre nos casos triviais de n=1 e n=2 onde a distancia é um proporçao direta formada por uma funçao linear.
2. isso para mim gera uma proporçao nao direta, diferente do que ocorre nos casos triviais de n=1 e n=2 onde a distancia é um proporçao direta formada por uma funçao linear. ![{D}_{} = \sqrt[]{{(x - x)}^{2} + {(y - y)}^{2}} {D}_{} = \sqrt[]{{(x - x)}^{2} + {(y - y)}^{2}}](/latexrender/pictures/813b779a606d9244692f21c93880efed.png) ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes n
ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes n  3 nao tem soluçao. isso prova o ultimo teorema de Fermat.
3 nao tem soluçao. isso prova o ultimo teorema de Fermat.

 .
.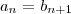
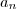 e
e 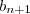 ficou confusa. Mas ao que parece, você deseja dizer que o número inteiro
ficou confusa. Mas ao que parece, você deseja dizer que o número inteiro 
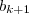 e
e 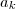
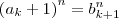

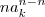 antes do 1, ao invés de
antes do 1, ao invés de 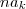 como deveria ser.
como deveria ser.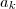 é antecessor de
é antecessor de 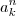 não será antecessor de
não será antecessor de 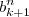 . Por exemplo, 5 é o antecessor de 6, mas 5² não é o antecessor de 6².
. Por exemplo, 5 é o antecessor de 6, mas 5² não é o antecessor de 6².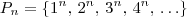
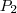 seria
seria 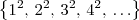 .
.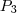 seria
seria  .
. .
. ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes
ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes  nao tem soluçao. isso prova o ultimo teorema de Fermat.
nao tem soluçao. isso prova o ultimo teorema de Fermat.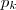 o k-ésimo termo da sequência
o k-ésimo termo da sequência 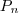 definida anteriormente. Teremos que
definida anteriormente. Teremos que  .
.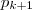 e
e 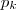 (dois termos consecutivos de
(dois termos consecutivos de 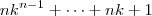 .
.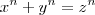 .
.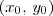 e
e 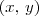 é dada por
é dada por  . Note que a expressão que você escreveu é na verdade equivalente a
. Note que a expressão que você escreveu é na verdade equivalente a 
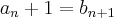 . usando a notaçao que vc indicou, façamos a verdadeira interpretaçao.
. usando a notaçao que vc indicou, façamos a verdadeira interpretaçao.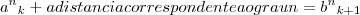 esses dois termos estao contidos na sequencia de grau n.
esses dois termos estao contidos na sequencia de grau n. 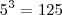 antecessor
antecessor 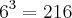 sucessor}.
sucessor}.