 por v0xxx » Sáb Dez 10, 2011 13:13
por v0xxx » Sáb Dez 10, 2011 13:13
Pensando numa solução pra um programa de computador cheguei a esta conclusão e funcionou perfeitamente. Mas gostaria de prová-la formalmente mas não tô conseguindo, se alguém ajudar eu agradeço. Segue a proposição:
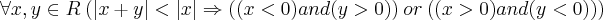
Basicamente o que diz é: Se a soma do módulo de 2 números reais for menor que o módulo do 1º deles, então os números tem sinais contrários.
Como disse, está certo, mentalmente eu consigo provar, mas formalmente não consigo

-
v0xxx
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 10, 2011 12:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Tecnologia da Informação
- Andamento: cursando
 por MarceloFantini » Dom Dez 11, 2011 04:00
por MarceloFantini » Dom Dez 11, 2011 04:00
Primeiro você quer dizer o módulo da soma, e não "soma do módulo de dois números reais", que seria algo como

. A condição de que tem sinais opostos pode ser simplificada para
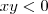
, ou seja, o produto é negativo.
Por último, não menos importante, um contra-exemplo: faça

e

. Então
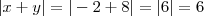
enquanto que

. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o
máximo dentre os dois, então eles tem sinais opostos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por v0xxx » Dom Dez 11, 2011 17:18
por v0xxx » Dom Dez 11, 2011 17:18
MarceloFantini escreveu:Primeiro você quer dizer o módulo da soma, e não "soma do módulo de dois números reais", que seria algo como

. A condição de que tem sinais opostos pode ser simplificada para
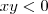
, ou seja, o produto é negativo.
Por último, não menos importante, um contra-exemplo: faça

e

. Então
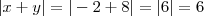
enquanto que

. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o
máximo dentre os dois, então eles tem sinais opostos.
Exato, é o módulo da soma, eu me enganei. E de fato a lógica está um pouquinho errada. O certo certo é:
Se o módulo da soma for menor que o
maior deles em módulo então eles tem sinais contrários

(porque se fosse
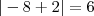
, que seria menor que
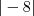
)
Muito obrigado!!!
-
v0xxx
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 10, 2011 12:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Tecnologia da Informação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- consigo na lógica mas na prática ta dificll
por Negte » Qui Fev 06, 2014 17:50
- 2 Respostas
- 1845 Exibições
- Última mensagem por Negte

Qui Fev 06, 2014 18:30
Álgebra Elementar
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 5802 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
-
- Pq será que não deu certo?
por Fernanda Lauton » Seg Jul 05, 2010 14:18
- 1 Respostas
- 1534 Exibições
- Última mensagem por Elcioschin

Seg Jul 05, 2010 15:06
Logaritmos
-
- L=R-C - Por favor, fiz certo ou não?
por HamiltonAN » Sex Jun 17, 2011 17:32
- 0 Respostas
- 1421 Exibições
- Última mensagem por HamiltonAN

Sex Jun 17, 2011 17:32
Álgebra Elementar
-
- Estou certo?
por Cleyson007 » Sáb Jun 09, 2012 13:01
- 1 Respostas
- 1545 Exibições
- Última mensagem por Molina

Sáb Jun 09, 2012 14:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
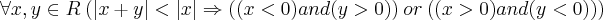


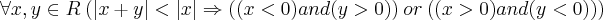


 . A condição de que tem sinais opostos pode ser simplificada para
. A condição de que tem sinais opostos pode ser simplificada para 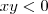 , ou seja, o produto é negativo.
, ou seja, o produto é negativo.  e
e  . Então
. Então 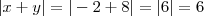 enquanto que
enquanto que  . Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o máximo dentre os dois, então eles tem sinais opostos.
. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o máximo dentre os dois, então eles tem sinais opostos.

. A condição de que tem sinais opostos pode ser simplificada para
, ou seja, o produto é negativo.
e
. Então
enquanto que
. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o máximo dentre os dois, então eles tem sinais opostos.
 (porque se fosse
(porque se fosse 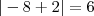 , que seria menor que
, que seria menor que 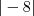 )
)