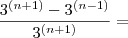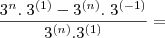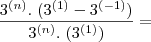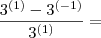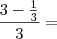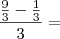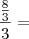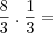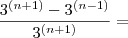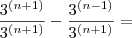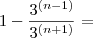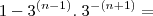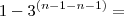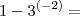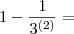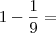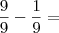por sinuca147 » Qui Mai 21, 2009 03:11
por sinuca147 » Qui Mai 21, 2009 03:11
Fiz testes com a equação

testando vários valores para n, e o resultado é sempre o mesmo, como posso simplificar ainda mais esta equação?
Obrigado.
Carlos Roberto Rodrigues Júnior
-
sinuca147
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Mai 14, 2009 01:36
- Localização: Belo Horizonte
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informática
- Andamento: cursando
 por Molina » Qui Mai 21, 2009 03:52
por Molina » Qui Mai 21, 2009 03:52
sinuca147 escreveu:Fiz testes com a equação

testando vários valores para n, e o resultado é sempre o mesmo, como posso simplificar ainda mais esta equação?
Obrigado.
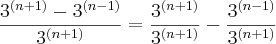
Coloquei aqui apenas o primeiro passo.
Vamos ver se assim você tem uma

e consegue fazer o resto sozinho.
Qualquer dúvida coloque aqui, ok?
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por sinuca147 » Qui Mai 21, 2009 15:12
por sinuca147 » Qui Mai 21, 2009 15:12
Carlos Roberto Rodrigues Júnior
-
sinuca147
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Mai 14, 2009 01:36
- Localização: Belo Horizonte
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificar equação
 por Fulgore » Sáb Mai 23, 2009 17:21
por Fulgore » Sáb Mai 23, 2009 17:21
- 1 Respostas
- 1406 Exibições
- Última mensagem por Neperiano

Dom Set 04, 2011 22:35
Álgebra Elementar
-
- Dúvida em simplificar equação
por Nooty » Seg Jul 07, 2014 02:05
- 2 Respostas
- 1439 Exibições
- Última mensagem por Nooty

Ter Jul 08, 2014 12:23
Equações
-
- [Geometria Analítica] Simplificar a equação
por esthinri » Qua Jun 04, 2014 12:59
- 0 Respostas
- 1238 Exibições
- Última mensagem por esthinri

Qua Jun 04, 2014 12:59
Geometria Analítica
-
- Simplificar
por Sandy26 » Ter Abr 27, 2010 14:35
- 5 Respostas
- 3178 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 18:29
Cálculo: Limites, Derivadas e Integrais
-
- Simplificar
por victorleme » Qua Mai 04, 2011 20:06
- 4 Respostas
- 2518 Exibições
- Última mensagem por victorleme

Qui Mai 05, 2011 18:56
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




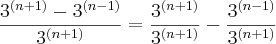
 e consegue fazer o resto sozinho.
e consegue fazer o resto sozinho.