 por bira19 » Qui Out 06, 2011 23:33
por bira19 » Qui Out 06, 2011 23:33
![\frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt[2]{5}+x \right)\sqrt[2]{x-2}} \frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt[2]{5}+x \right)\sqrt[2]{x-2}}](/latexrender/pictures/a340c062300daafd210072e4734624a6.png)
Não consigo simplificar para eliminar raizes, como resolver?
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
 por bira19 » Dom Out 09, 2011 17:47
por bira19 » Dom Out 09, 2011 17:47
Obrigado.
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- simplificação de expressões
por bianca12 » Qui Out 03, 2013 13:56
- 0 Respostas
- 782 Exibições
- Última mensagem por bianca12

Qui Out 03, 2013 13:56
Probabilidade
-
- simplificação de expressões
por bianca12 » Qui Out 03, 2013 14:07
- 1 Respostas
- 1024 Exibições
- Última mensagem por Bravim

Qui Out 03, 2013 16:48
Análise Combinatória
-
- Simplificação de raizes
por LuizCarlos » Sáb Mai 05, 2012 00:14
- 3 Respostas
- 2330 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 14:00
Álgebra Elementar
-
- Simplificação de raízes.
por Sobreira » Qui Mai 09, 2013 22:21
- 1 Respostas
- 1320 Exibições
- Última mensagem por brunnkpol

Qui Mai 09, 2013 23:49
Aritmética
-
- simplificação de raízes
por ezidia51 » Seg Mar 12, 2018 23:39
- 2 Respostas
- 2766 Exibições
- Última mensagem por ezidia51

Ter Mar 13, 2018 12:21
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt[2]{5}+x \right)\sqrt[2]{x-2}} \frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt[2]{5}+x \right)\sqrt[2]{x-2}}](/latexrender/pictures/a340c062300daafd210072e4734624a6.png)

![\frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt[2]{5}+x \right)\sqrt[2]{x-2}} \frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt[2]{5}+x \right)\sqrt[2]{x-2}}](/latexrender/pictures/a340c062300daafd210072e4734624a6.png)

![\frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt{5}+x \right)\sqrt{x-2}} = \frac{\left[\left(5-{x}^{2} \right)3x\left(2x-4 \right)\right]\cdot \left(\sqrt{5}-x \right)}{\left[\left(\sqrt{5}+x \right)\sqrt{x-2}\right]\cdot \left(\sqrt{5}-x \right)} \frac{\left(5-{x}^{2} \right)3x\left(2x-4 \right)}{\left(\sqrt{5}+x \right)\sqrt{x-2}} = \frac{\left[\left(5-{x}^{2} \right)3x\left(2x-4 \right)\right]\cdot \left(\sqrt{5}-x \right)}{\left[\left(\sqrt{5}+x \right)\sqrt{x-2}\right]\cdot \left(\sqrt{5}-x \right)}](/latexrender/pictures/50b800c1db2ef6d2d2e62db5eed02391.png)
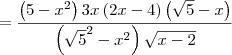
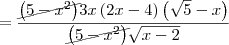
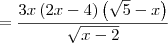
![= \frac{\left[3x\left(2x-4 \right)\left(\sqrt{5}-x \right)\right]\cdot \sqrt{x-2}}{\left(\sqrt{x-2}\right)\cdot \sqrt{x-2}} = \frac{\left[3x\left(2x-4 \right)\left(\sqrt{5}-x \right)\right]\cdot \sqrt{x-2}}{\left(\sqrt{x-2}\right)\cdot \sqrt{x-2}}](/latexrender/pictures/7bdf7d74b29495bace1d619676c6ddea.png)
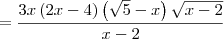
![= \frac{3x\left[2(x-2)\right]\left(\sqrt{5}-x \right)\sqrt{x-2}}{x-2} = \frac{3x\left[2(x-2)\right]\left(\sqrt{5}-x \right)\sqrt{x-2}}{x-2}](/latexrender/pictures/5c0d5854ecb7717669fe421a30cf5140.png)
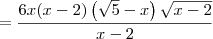
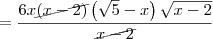
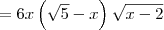




 , avisa que eu resolvo.
, avisa que eu resolvo.

