respectivamente. O preço x que o comerciante paga por uma calça é três vezes o que ele paga por uma
camisa e duas vezes o que ele paga por uma saia.
Um certo dia, um cliente comprou duas calças, duas camisas e duas saias e obteve um desconto de 10%
sobre o preço total.
b) Qual o lucro aproximado, em porcentagem, obtido pelo comerciante nessa venda?
SEI QUE O CLIENTE PAGOU PELA COMPRA = 4,17x
O preço de custo dos produtos vendidos foi:
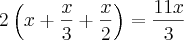
Lucro = Venda - Custo
4,17x -
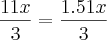 , correspondendo a
, correspondendo a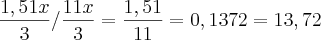 %
%PQ É DIVIDIDO O LUCRO PELO CUSTO???? NÃO DEVERIA SER FEITO REGRA DE 3????


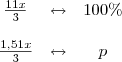
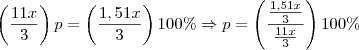
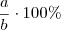 . Por exemplo, a porcentagem que 2 representa de 5 é
. Por exemplo, a porcentagem que 2 representa de 5 é 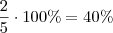 .
.
