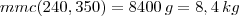por hevhoram » Seg Mai 16, 2011 16:59
por hevhoram » Seg Mai 16, 2011 16:59
Uma empresa confeccionou catálogos dos tipos A e B para presentear seus clientes. Um catálogo tipo A pesa 240 g e um do tipo B, 350g. Os catálogos foram organizados em pacotes, contendo cada um deles apenas catálogos de um mesmo tipo.
Com base nas informações do texto, é correto afirmar que, se todos os pacotes tiverem o mesmo peso e se esse peso for inferior a 10kg, então cada pacote pesará
A) 8,2 kg
B) 8,3 kg
C) 8,4 kg
D) 8 kg
E) 8,1 kg
(tentei fazer pelo mdc: mais nao entendi como proceder ????) daí nao sei nem por onde tentar???
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por FilipeCaceres » Seg Mai 16, 2011 17:09
por FilipeCaceres » Seg Mai 16, 2011 17:09
Faça
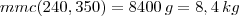
Espero que seja isso.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão fácil, me ajuda, concurso correios 2011 cesp, obriga
por jrmaialds » Seg Nov 12, 2012 16:40
- 2 Respostas
- 2701 Exibições
- Última mensagem por jrmaialds

Seg Nov 12, 2012 18:03
Aritmética
-
- Medida de massa - apostila p/ concurso dos correios
por Igra » Seg Abr 22, 2013 10:49
- 0 Respostas
- 2424 Exibições
- Última mensagem por Igra

Seg Abr 22, 2013 10:49
Conversão de Unidades
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10974 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15116 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.