Podem me ajudar a responder essa questão, ou pelo menos me dar alguma dica?
Construa uma bijeção entre o conjunto dos números naturais e o conjunto de todas as parábolas que passam pela origem e que tenham seus coeficientes números inteiros positivos. O que você pode afirmar sobre a enumerabilidade do conjunto das parábolas? Justifique a sua resposta.
Dei a seguinte resposta:
Bijeção: Cada elemento da imagem corresponde a um e somente um elemento no domínio e vice versa, no caso específico desta questão:
y Pertente aos N* , isso é, o conjunto Imagem do cojunto de todas as parábolas que passam pela origem e tem coeficientes números inteiros positivos.
Conjunto de Todas as Parábolas que passam pela origem com coeficientes números inteiros positivos, ou seja , qualquer q seja a e b pertencentes aos N* : y=ax^2 +bx
Como os coeficientes a e b são números inteiros positivos, determinei: a=2 e b=3
Para que haja uma bijeção com os Naturais é necessário que y pertence N , e nesse caso teremos:
y=2x^2+bx com y pertencendo a N teremos y={1,2,3,4,...}
resolvendo y=0 -> 0=2x^2+3x temos 0=x(2x+3) que x=(-3/2,0) para y=1 temos x=(-1,1) e assim por diante...
Porém como qq que seja a,b eles pertencem a N*, então vamos testar com a=5 e b=7: y = 5x^2+ 7x, pois esta equação de parábola também passa pela origem, logo:
0=5x^2+7x 0=x(5x+7) x=(-7/5,0) e assim por diante...
Como ambas as equações e y = 5x^2+ 7x ^2+3x passam pela origem podemos concluir, a partir delas, que o conjunto de todas as parábolas que passam pela origem NÃO é uma bijeção com os Naturais, isso pois há mais de uma correspondência no Domínio para o mesmo elemento da Imagem.
Logo concluímos que o conjunto das parábolas que passam pela origem não é enumerável, pois para isso seria necessário que este mesmo conjunto fosse uma bijeção com os Naturais, o que acabamos de provar que não é.
Resposta da professora:
Inicialmente observo que sempre que você se refere à forma ax^2+bx, lembre-se de que a deve ser diferente de zero, pois caso contrário não é parábola. Todas as contas que você fez não justificam. Veja que basta que haja uma bijeção para que eu possa garantir que é enumerável. O fato de você não ter conseguido uma bijeção não garante que essa sua escolha foi adequado ao processo
.
Bibiana
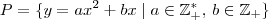. Note que 
.
