A)24 b)36 c)40 d)44
O raciocinio que tive no exercicio>
Legenda> x=divisor y=quociente r=resto
xy+r=90
xy+2y=90
xy=90-2y
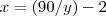
temos que
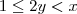 ,pois o resto nao pode ser maior que o divisor nem menor que 1
,pois o resto nao pode ser maior que o divisor nem menor que 1seguindo esse raciocinio,percebo que o valor maximo de y é 6 e que o valor minimo de y é 0.5,aplicando isso,n,valeria 12
o gabarito é resposta letra A
Por favor alguem reporte meu erro,eu tentei fazer de tudo que sei,como sao varios raciocinios diferentes,nao acho relevante colocar todos aqui,sendo que tudo que tentei a resposta da n=12
Sobre o titulo do topico,a materia estudada é sobre conjuntos,mas nao sei se enquandra muito em conjuntos,por isso nao dei certeza


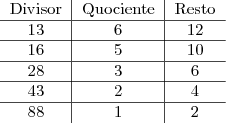

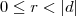 (perceba que o resto é sempre positivo e pode ser nulo!).
(perceba que o resto é sempre positivo e pode ser nulo!).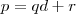 ,
,  deve ser inteiro e não racional (ou melhor, racional com denominador diferente de 1).
deve ser inteiro e não racional (ou melhor, racional com denominador diferente de 1).

 .
.



