 por Pedro123 » Sáb Mar 26, 2011 23:18
por Pedro123 » Sáb Mar 26, 2011 23:18
Fala fabricio.
Primeira coisa a fazer é organizar a equação:
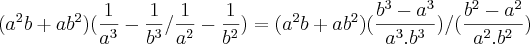
temos então que
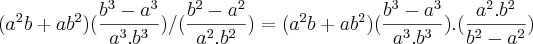
que por sua vez é igual a:
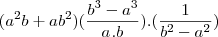
porem, temos que
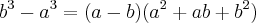
e
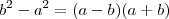
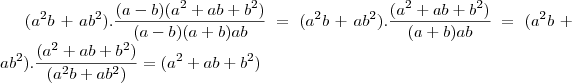
Portanto e finalmente (ufa!), depois de alguma macumbinha algebrica temos que:
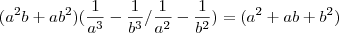
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto notável
por matmatco » Ter Nov 19, 2024 07:39
- 5 Respostas
- 5087 Exibições
- Última mensagem por DanielFerreira

Seg Dez 16, 2024 20:44
Álgebra Elementar
-
- [Produto notavel com Radiciaçao(Polinômios)]
por Fabricio dalla » Qui Dez 08, 2011 13:11
- 1 Respostas
- 2280 Exibições
- Última mensagem por MarceloFantini

Qui Dez 08, 2011 22:00
Polinômios
-
- Matémática básica
por drea70br » Dom Out 04, 2009 20:59
- 1 Respostas
- 6175 Exibições
- Última mensagem por Elcioschin

Dom Out 04, 2009 21:10
Álgebra Elementar
-
- matematica básica
por gilson » Qui Mai 30, 2013 00:43
- 3 Respostas
- 13946 Exibições
- Última mensagem por Rafael16

Qui Mai 30, 2013 19:31
Pedidos de Materiais
-
- problema de matematica basica
por Aline » Qua Abr 22, 2009 19:00
- 2 Respostas
- 5949 Exibições
- Última mensagem por Aline

Qua Abr 22, 2009 19:24
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\frac{{[(a+b)(a-b)]}^{2}.ab.({b}^{2}+ab+{a}^{2})}{{ab}^{3}} \frac{{[(a+b)(a-b)]}^{2}.ab.({b}^{2}+ab+{a}^{2})}{{ab}^{3}}](/latexrender/pictures/debcf59cb63ae2d30bba82f8dbf0bc0f.png)


![\frac{{[(a+b)(a-b)]}^{2}.ab.({b}^{2}+ab+{a}^{2})}{{ab}^{3}} \frac{{[(a+b)(a-b)]}^{2}.ab.({b}^{2}+ab+{a}^{2})}{{ab}^{3}}](/latexrender/pictures/debcf59cb63ae2d30bba82f8dbf0bc0f.png)

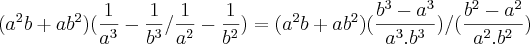
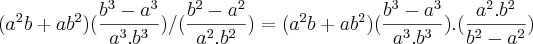
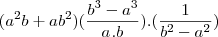
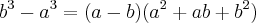
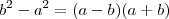
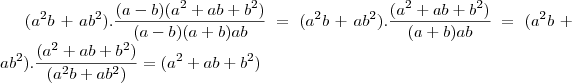
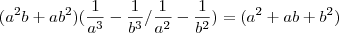


 .
.



