 por Abelardo » Seg Mar 07, 2011 04:50
por Abelardo » Seg Mar 07, 2011 04:50
A equação
![\sqrt[]{x+10} - \sqrt[]{2x+3}=\sqrt[]{1-3x} \sqrt[]{x+10} - \sqrt[]{2x+3}=\sqrt[]{1-3x}](/latexrender/pictures/c6c1cb92984617e597864f31b3c24367.png)
a)não tem solução
b)tem uma única solução positiva
c)tem uma única solução negativa
d)tem duas soluções uma positiva e outra negativa
e)tem duas soluções ambas negativas
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Adriano Tavares » Seg Mar 14, 2011 22:48
por Adriano Tavares » Seg Mar 14, 2011 22:48
Olá,Abelardo.
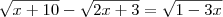
Elevando ambos os membros ao quadrado teremos:
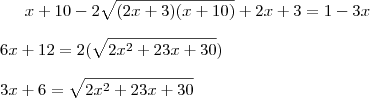
Elevando novamente ambos os membros ao quadrado teremos:
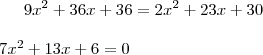
Resolvendo essa equação encontraremos
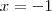
ou

Substituindo os valores de

verifica-se que ambos satisfazem a equação
Alternativa:e
-
Adriano Tavares
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Mar 07, 2011 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em automação industrial
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Lógica - OBM de 1997
por Abelardo » Seg Mar 07, 2011 04:27
- 4 Respostas
- 2582 Exibições
- Última mensagem por Renato_RJ

Seg Mar 07, 2011 15:13
Álgebra Elementar
-
- Lógica - OBM de 1997 (2)
por Abelardo » Seg Mar 07, 2011 04:38
- 0 Respostas
- 611 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 04:38
Álgebra Elementar
-
- Lógica - OBM de 1997 (3)
por Abelardo » Seg Mar 07, 2011 04:41
- 1 Respostas
- 1072 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 04:55
Álgebra Elementar
-
- [números complexos] (fuvest 1997)
por JKS » Dom Set 23, 2012 01:35
- 1 Respostas
- 1419 Exibições
- Última mensagem por young_jedi

Dom Set 23, 2012 14:00
Números Complexos
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 5802 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{x+10} - \sqrt[]{2x+3}=\sqrt[]{1-3x} \sqrt[]{x+10} - \sqrt[]{2x+3}=\sqrt[]{1-3x}](/latexrender/pictures/c6c1cb92984617e597864f31b3c24367.png)

![\sqrt[]{x+10} - \sqrt[]{2x+3}=\sqrt[]{1-3x} \sqrt[]{x+10} - \sqrt[]{2x+3}=\sqrt[]{1-3x}](/latexrender/pictures/c6c1cb92984617e597864f31b3c24367.png)

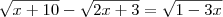
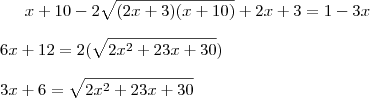
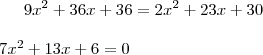
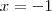 ou
ou 
 verifica-se que ambos satisfazem a equação
verifica-se que ambos satisfazem a equação