 por VtinxD » Qua Fev 09, 2011 02:11
por VtinxD » Qua Fev 09, 2011 02:11
Estou com este problema que não consigo resolver,agradeço desde já a ajuda:
O numero
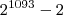
divisivel por
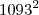
?
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por Renato_RJ » Qua Fev 16, 2011 00:13
por Renato_RJ » Qua Fev 16, 2011 00:13
Cara, pesquisando eu descobri os números primos de Wieferich, que diz o seguinte:
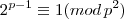
Dividindo por 2, teremos:
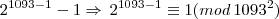
Posso ter me enganado, ainda não me entendi muito bem com essa disciplina (teoria dos números) então é melhor esperar alguém mais experiente (molina ou o prof. Luiz Aquino) olharem o tópico, mas acho que é "por aí" a tua resposta....
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisibilidade
por victoreis1 » Qua Out 20, 2010 14:59
- 5 Respostas
- 3875 Exibições
- Última mensagem por VtinxD

Qui Out 21, 2010 21:49
Desafios Médios
-
- Divisibilidade
por igorcamilo » Sex Jun 24, 2011 19:20
- 1 Respostas
- 1207 Exibições
- Última mensagem por FilipeCaceres

Sex Jun 24, 2011 19:40
Álgebra Elementar
-
- [DIVISIBILIDADE]
por juliohenriquelima14 » Sáb Dez 13, 2014 23:20
- 1 Respostas
- 1464 Exibições
- Última mensagem por adauto martins

Dom Dez 21, 2014 11:49
Aritmética
-
- Divisibilidade
por Lucio » Sáb Fev 25, 2017 10:41
- 1 Respostas
- 1988 Exibições
- Última mensagem por petras

Qua Mar 08, 2017 19:30
Aritmética
-
- Divisibilidade, congruência
por ckde » Seg Ago 02, 2010 10:42
- 0 Respostas
- 1196 Exibições
- Última mensagem por ckde

Seg Ago 02, 2010 10:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
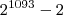 divisivel por
divisivel por 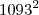 ?
?
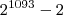 divisivel por
divisivel por 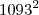 ?
?
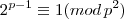
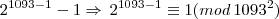


 .
.



