por Renato_RJ » Ter Fev 15, 2011 00:19
por Renato_RJ » Ter Fev 15, 2011 00:19
Boa noite a todos, gostaria da correção dos colegas no desenvolvimento da questão abaixo, eu fiz, mas não sei se está certo ou se falta algum detalhe na demonstração, poderiam verificar ?
Dados
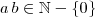
. Aplicamos sucessivamente o algoritmo de Euclides temos:
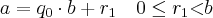
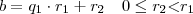
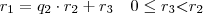

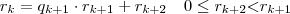
Como

. Temos que existe um primeiro inteiro s tal que
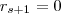
. Prove que
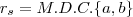
.
O que eu fiz:
Extrapolando o algoritmo temos:

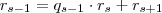
Usando o teorema abaixo:
"Se
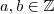
e
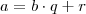
onde
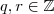
então

"
Teremos:
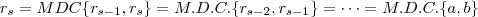
A minha demonstração está correta ? A linguagem também ?
Grato,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
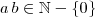 . Aplicamos sucessivamente o algoritmo de Euclides temos:
. Aplicamos sucessivamente o algoritmo de Euclides temos: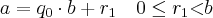
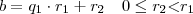
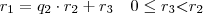

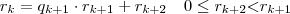
 . Temos que existe um primeiro inteiro s tal que
. Temos que existe um primeiro inteiro s tal que 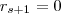 . Prove que
. Prove que 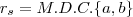 .
.
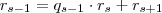
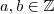 e
e 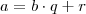 onde
onde 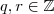 então
então  "
"