 por Renato_RJ » Sáb Jan 08, 2011 01:37
por Renato_RJ » Sáb Jan 08, 2011 01:37
Caros colegas, alguém poderia verificar se eu fiz a questão de forma correta ? Serei muito grato...
Prove que

é divisível por 7.
Eu fiz assim:
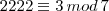
Logo:
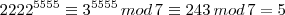
Aqui eu estudei o ciclo de repetições do último algarismo das potências de 3, como abaixo:
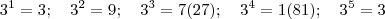
e assim em diante.
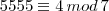
Logo:
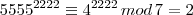
Aqui usei o mesmo procedimento de estudo do ciclo de repetições do último algarismo, mas para as potências de 4.
Então temos:
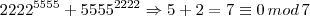
Então, estaria provado que a soma é divisível por 7.
Esse raciocínio está correto ?
Grato,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por VtinxD » Sáb Jan 08, 2011 09:06
por VtinxD » Sáb Jan 08, 2011 09:06
Acho que seu raciocínio esta correto mas acho que uma resolução mais elegante seria usar o pequeno teorema de Fermat ao invés de estudar os ciclos*.
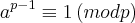
*Na verdade é provavelmente onde ele percebeu o teorema dele.
Espero ter ajudado e bons estudos ,esta matéria é muito legal

.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por Renato_RJ » Sáb Jan 08, 2011 12:07
por Renato_RJ » Sáb Jan 08, 2011 12:07
Interessante, uma abordagem diferente ao mesmo problema.. Vou fazer segundo a sua recomendação e posto aqui para discutirmos.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17196 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Teoria dos Números
por cheese » Sáb Out 24, 2009 14:08
- 1 Respostas
- 2245 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2009 15:10
Álgebra Elementar
-
- Teoria dos números!
por Abelardo » Qui Mar 10, 2011 01:44
- 0 Respostas
- 1572 Exibições
- Última mensagem por Abelardo

Qui Mar 10, 2011 01:44
Álgebra Elementar
-
- Teoria dos Números
por felipemaster » Qua Jul 06, 2011 12:26
- 1 Respostas
- 2065 Exibições
- Última mensagem por MarceloFantini

Qua Jul 06, 2011 19:41
Álgebra Elementar
-
- Teoria dos Números
por Jamyson » Seg Jan 21, 2013 19:28
- 1 Respostas
- 3723 Exibições
- Última mensagem por young_jedi

Qui Jan 24, 2013 21:49
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é divisível por 7.
é divisível por 7.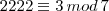
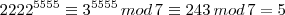
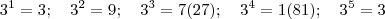 e assim em diante.
e assim em diante.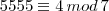
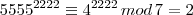
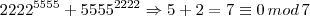


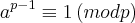
 .
.

 .
.



