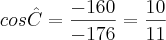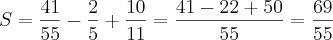Unifei - prova3 2007
Olá gente
vou fazer o vestibular da unifei este final de semana, e qdo fui dar uma conferida na prova dissertativa de matematica, fornecida por eles, mal conseguia responder as questoes e mto menos entender as respostas dadas por eles, ou conseguir seguir a linha de raciocinio para chegar nestes resultados, gostaria de saber se ninguen poderia fazer as resoluçoes dessa prova, sao 10 questoes
http://www.vestibular.unifei.edu.br/arquivos_upload/provas/2007/Prova%203%20-%202007%20-%20Matematica.doc
se tiver como fazer essas resoluçoes de modo q seja possivel compreender
obrigado ^^
vou fazer o vestibular da unifei este final de semana, e qdo fui dar uma conferida na prova dissertativa de matematica, fornecida por eles, mal conseguia responder as questoes e mto menos entender as respostas dadas por eles, ou conseguir seguir a linha de raciocinio para chegar nestes resultados, gostaria de saber se ninguen poderia fazer as resoluçoes dessa prova, sao 10 questoes
http://www.vestibular.unifei.edu.br/arquivos_upload/provas/2007/Prova%203%20-%202007%20-%20Matematica.doc
se tiver como fazer essas resoluçoes de modo q seja possivel compreender
obrigado ^^
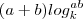

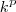
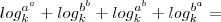






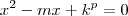
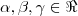 ,
, 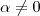 .
.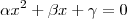
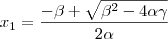

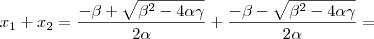
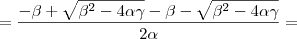
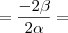
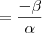
 e
e 
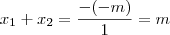
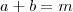 (passo
(passo 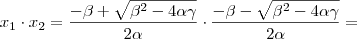
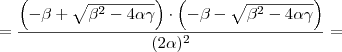


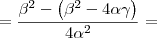
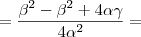
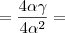

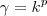 e
e 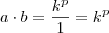 (passo
(passo 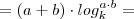


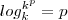
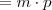 (que é o 2o. membro, onde queríamos chegar)
(que é o 2o. membro, onde queríamos chegar)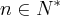 :
: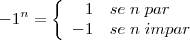
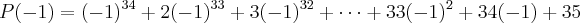

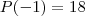
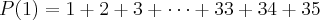
 :
: