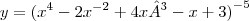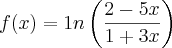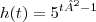... voce tem f(x)=x-2 , então a partir do gráfico de f(x)=x voce percebesse o que acontece quando é atribuido um valor negativo a essa função. Você sabe que o gráfico de f(x)=x corta o gráfico nos pontos (-n, -n) ... (0,0) (1,1) (2,2) ... (n,n). Quando colocado um valor negativo ...


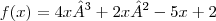 , calcule f"(0)+f'''(0).
, calcule f"(0)+f'''(0).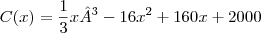 .Determinar o ponto de mínimo do custo marginal.
.Determinar o ponto de mínimo do custo marginal.![f(x)={x}^{4}.(\sqrt[]{3x-7} f(x)={x}^{4}.(\sqrt[]{3x-7}](/latexrender/pictures/26f1364c5ac962034ad79e1de19a8ed8.png)
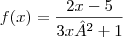
![y=4.\sqrt[5]{x³} y=4.\sqrt[5]{x³}](/latexrender/pictures/d07dafc5126c78a5146fb60ade332c4b.png)